- ONDES (physique)
- ONDES (physique)Le concept d’onde est l’un des plus universels de la physique mathématique. Ce dernier, élaboré au XVIIe siècle, lorsque la division entre mathématiques et physique (et philosophie aussi) n’avait pas le caractère institutionnel que nous lui connaissons, est né de l’observation d’un phénomène des plus ordinaires: la propagation d’ondes ou de rides à la surface de l’eau (les mots wave en anglais et Welle en allemand désignent aussi bien une onde qu’une vague). Alors que le concept d’onde envahissait progressivement tous les domaines de la physique, au point de devenir l’un des deux concepts ontologiques fondamentaux de la physique classique, se développait l’étude de ses propriétés proprement mathématiques, étude liée aux travaux du XVIIIe siècle sur les équations aux dérivées partielles. À l’heure actuelle, la situation est telle qu’un physicien et un mathématicien, parlant d’«ondes», ont besoin de s’assurer qu’ils parlent bien de la même chose. D’où la structure du présent article, divisé en deux parties, l’une «physique», exposant les principales caractéristiques du concept tel qu’il est défini traditionnellement en physique, l’autre «mathématique», où l’accent est porté sur les récents développements de l’étude mathématique des ondes.En dehors des rides à la surface de l’eau, archétype pédagogique, le concept d’onde permet de parler en termes physico-mathématiques de phénomènes aussi divers que le son (ondes sonores considérées comme des ondes de pression se propageant dans l’air), ou que la lumière (de nature électromagnétique, combinaison de deux champs, électrique et magnétique, dont le couplage est régi par les équations de Maxwell). On parlera également en termes d’ondes de la propagation des ébranlements dans les solides; dans ce cas, il peut s’agir soit d’une onde de compression (modélisée par la compression des «ressorts» liant les wagons d’un train, se propageant d’un bout à l’autre du train lorsqu’on y accroche une locomotive), soit d’ondes d’oscillation, lesquelles peuvent être soit longitudinales (les atomes vibrant alors le long de la direction de propagation), soit transversales (les atomes vibrant dans un plan perpendiculaire à cette même direction). Par exemple, les ondes sismiques qui se propagent dans la croûte terrestre lors d’un tremblement de terre sont de compression et d’oscillation. Toujours dans le domaine classique, on parlera d’ondes de choc pour désigner le sillage qui accompagne le mouvement d’une source émettrice d’ondes: sillage d’un bateau sur la mer, bien sûr, mais également sillage sonore d’un avion se déplaçant à une vitesse supersonique ou sillage (dit de Cerenkov) d’une particule chargée en mouvement rapide.L’application du concept d’onde à des domaines aussi vastes que divers traduit simplement le fait que des équations de même type admettent des solutions de même type, indépendamment de la nature physique des grandeurs dont les êtres mathématiques, figurant dans ces équations, sont les représentants. C’est pourquoi l’on s’intéressera plus dans l’analyse qui suit aux déterminations du concept d’onde qu’à la description de ses divers champs d’application. Ce faisant, on ne saurait oublier que le concept d’onde n’est pas un concept mathématique et ne peut donc, en aucun cas, se résumer à l’étude mathématique des équations (dites équations d’ondes) qui régissent les phénomènes ondulatoires.En physique classique, les concepts d’onde et de particule vont nécessairement de pair et lorsqu’il apparut, au début de ce siècle, que la physique classique ne permettait pas de rendre compte de phénomènes que les progrès techniques rendaient observables, les notions d’onde et de particule durent, ensemble, être soumises à une révision – révision déchirante du fait de l’universalité de ces deux concepts.Cependant, tout au long de l’élaboration de la dualité onde-corpuscule, vint à naître l’idée que le concept d’onde (tout comme celui de particule) n’a, à proprement parler, de sens que dans le domaine classique, numériquement délimité par référence à la constante quantique, dite de Planck, h . C’est pourquoi des expressions telles que «longueur d’onde de De Broglie associée à une particule», ou «fonction d’onde» ne doivent pas être prises au pied de la lettre: il n’y a pas d’onde dans le domaine quantique et, si le mot «onde» y intervient, ce n’est que de façon métaphorique.1. Histoire du concept d’ondeLa signification du concept d’onde ne peut se comprendre sans référence à l’histoire: il n’est pas né armé de toutes ses propriétés, prêt à l’«usage» que nous en faisons aujourd’hui; il a été forgé au cours de l’histoire de la physique, par ajouts et rectifications successifs. On peut distinguer, dans ce développement, trois temps forts.Naissance du concept«Quand on considère», écrit Christiaan Huygens dans son Traité de la lumière (1690), «l’extrême vitesse dont la lumière s’étend de toutes parts et que [...] quand il en vient [des lumières] de différents endroits, même de tout opposés, elles se traversent l’une l’autre sans s’empêcher, on comprend bien que, quand nous voyons un objet lumineux, ce ne saurait être par le transport d’une matière, qui depuis cet objet s’en vient jusqu’à nous ainsi qu’une balle ou une flèche traverse l’air [...]. C’est donc d’une autre manière que [la lumière] s’étend, et ce qui nous conduit à la comprendre, c’est la connaissance que nous avons de l’extension, du son dans l’air».Le concept d’onde a donc pour origine une critique de la conception corpusculaire de la lumière, laquelle ne permet pas de comprendre le fait que deux «lumières» se croisent sans en être affectées, contrairement à ce qui se passe pour deux particules qui rebondissent l’une sur l’autre lorsque leurs chemins se croisent.Mais Huygens ne s’écarte pas pour autant de la «vraie philosophie dans laquelle on conçoit tous les effets naturels par des raisons de mécanique». Aussi les ondes ne sont-elles qu’une sorte de mouvement , différent du mouvement balistique attribué jusqu’alors aux corpuscules; les ondes, contrairement aux particules, ne sont pas des choses; elles n’acquéreront que plus tard le statut ontologique que nous leur connaissons.Le nouvel état de mouvement que représente le concept d’onde est décrit par Huygens par référence aux connaissances sur la propagation du son: «Nous savons que par le moyen de l’air, qui est un corps invisible et impalpable, le son s’étend tout à l’entour du lieu où il a été produit, par un mouvement qui passe successivement d’une partie de l’air à l’autre, et que, l’extension de ce mouvement se faisant également vite de tous côtés, il se doit former comme des surfaces sphériques qui s’élargissent toujours et qui viennent frapper notre oreille... Ce mouvement imprimé à la matière est successif et par conséquent il s’étend par des surfaces et des ondes sphériques: car je les appelle ondes, à la ressemblance de celles que l’on voit se former dans l’eau quand on y jette une pierre...»Cette description, pour conforme à l’intuition qu’elle soit, ne permet pas de comprendre ni ce qui a motivé l’invention du concept – à savoir le fait que deux lumières ne s’entrechoquent pas –, ni par quel mécanisme ce mouvement étendu s’entretient. Aussi Huygens ajoute-t-il à sa description phénoménologique deux «principes» explicatifs.– Le principe dit aujourd’hui de superposition : les ondes «se traversent l’une l’autre sans s’empêcher» et «s’unissent de sorte que sensiblement elles se composent en une seule onde».– Le principe dit, aujourd’hui encore, de Huygens : les ondes s’auto-engendrent par multiplication, le produit de deux ondes étant encore une onde. «Autour de chaque particule de la matière dans laquelle l’onde s’étend, [il se fait] une onde dont cette particule est le centre» (fig. 1). L’onde en un point donné est la superposition des «ondelettes» émises par les divers points.L’onde devient un concept physico-mathématiqueLa physique de Huygens est une physique sans équation, une représentation géométrique sans échelle et sans mesure. Il faut attendre le XIXe siècle pour que, avec Thomas Young et Augustin Fresnel, les ondes deviennent mesurables, par leur longueur d’onde, et calculables, par l’introduction du concept d’amplitude complexe.La principale difficulté présentée par la conception de Huygens se situe dans l’interprétation, à l’intérieur même de l’énoncé du principe de superposition, de l’expression «se composent en une seule onde». Très vite, il est apparu que cette composition n’était pas la pure et simple addition de deux nombres «ordinaires». En effet, on observe que deux ondes se superposant en un même point peuvent donner soit un renforcement, soit une diminution de l’intensité (lumineuse, par exemple). Ce phénomène est désigné sous le nom d’«interférence», terme qui marque bien la différence de nature entre cette «addition» et l’addition des nombres réels: au lieu de rester identiques à elles-mêmes, comme c’est le cas lors de l’addition de deux grandeurs réelles, les ondes «interfèrent» entre elles; tout se passe comme s’il y avait «influence mutuelle» (l’expression est de Fresnel lui-même).Dans son célèbre Mémoire sur la diffraction (1819), Fresnel propose de considérer l’addition des ondes sur le mode de celle des forces, c’est-à-dire comme une addition de vecteurs: «... l’onde résultant du concours des deux autres, écrit Fresnel, répond exactement, pour son intensité et pour sa direction, à la résultante de deux forces égales aux intensités des deux faisceaux lumineux, et faisant entre elles un angle qui soit à la circonférence entière comme l’intervalle qui sépare les deux systèmes d’ondes à la longueur d’une ondulation». Cette phrase, un peu difficile à comprendre, marque une révolution dans la représentation des grandeurs physiques. Jusqu’alors, en effet, une grandeur qui n’était pas purement géométrique était assimilée à un nombre réel; Fresnel, lui, établit que les ondes ne peuvent être représentées que par ce que nous reconnaissons, après coup, comme étant des nombres complexes , ou imaginaires comme l’on disait à l’époque; «après coup», car l’«invention» des nombres complexes par Carl Friedrich Gauss date de 1831. C’est l’amplitude ondulatoire, nombre complexe muni d’une phase , qu’introduit Fresnel par la phrase citée plus haut (à vrai dire, la terminologie du physicien est sur ce point ambiguë: amplitude signifie soit amplitude complexe, a ei size=1﨏, soit module de cette même amplitude complexe, a ). Cette phase 﨏 est présentée comme l’angle que font les deux «forces» à combiner; angle d’une nature particulière toutefois puisqu’il est défini non pas comme l’angle de deux droites, mais par la valeur de son rapport «à la circonférence entière», autrement dit par son rapport au tour complet: 2 神. Transcrite en termes modernes, la phrase de Fresnel se lit simplement:
 où désigne la «longueur d’une ondulation» – encore appelée la longueur d’onde – et 嗀 «l’intervalle qui sépare les deux systèmes d’ondes», la différence de marche, dirions-nous aujourd’hui.Ce faisant, Fresnel introduit une échelle dans la notion d’onde, échelle qui justement faisait défaut antérieurement. La longueur d’onde est la longueur caractéristique, l’aune à laquelle doivent être référées toutes les longueurs à considérer dans le phénomène de propagation. Après 1809, les expériences portant sur les ondes se ramèneront toutes à des mesures de longueur d’onde.Dès lors, le concept d’onde est établi en tant qu’objet physico-mathématique; une onde est caractérisée par son amplitude, nombre complexe dont le module est lié à l’intensité et dont la phase régit les combinaisons avec d’autres ondes. À partir de ce moment, les ondes acquièrent un statut ontologique, comparable, bien qu’en un certain sens opposé, à celui des particules.Champ et onde: le concept perd sa «matérialité»À l’origine, le concept d’onde est lié à un mouvement, mouvement vibratoire d’une particule source, provoquant un ébranlement du milieu dans lequel elle se trouve. Dans le cas du son, l’identification de ce milieu ne pose guère de problème: il s’agit de l’air, et la propagation du son s’effectue par mise en branle successive des couches d’air entre la source et le récepteur. «Maintenant, écrit Huygens dans le Traité de la lumière , si l’on examine quelle peut être cette matière dans laquelle s’étend le mouvement qui vient des corps lumineux, laquelle j’appelle éthérée, on verra que ce n’est pas la même qui sert à la propagation du son.» Pendant deux siècles, jusqu’à ce qu’en 1905 Albert Einstein en énonce l’inutilité, le concept d’éther devait apparaître comme indissociable d’abord des ondes lumineuses, puis des ondes électromagnétiques, lorsqu’il fut reconnu que la lumière n’en était qu’une forme particulière.Cet abandon de l’éther, milieu matériel progressivement dépouillé de toutes ses caractéristiques... matérielles, fut grandement facilité, voire suscité, par l’émergence progressive du concept de champ . Initialement, ce dernier est apparu comme un substitut à l’«action à distance», notion aux connotations occultes difficilement acceptables: plutôt que de dire qu’une particule – la Terre par exemple – agit à distance sur une autre – la Lune –, on préféra dire que la première particule induit, par sa seule présence, une modification de l’espace qui l’entoure et que c’est l’effet de cette modification, nommée champ , sur la deuxième qui produit la force que semble exercer à distance la première particule sur la deuxième. De plus, pour éviter d’avoir à penser une action, non seulement «à distance», mais qui plus est instantanée, on en vint à imaginer que le champ se propageait de proche en proche... tout comme une onde, dans un milieu qui, dans la plupart des cas, ne pouvait être que l’éther. Il apparut cependant très vite, avant même qu’Einstein en fasse le constat officiel, que l’éther n’était pas vraiment nécessaire à la compréhension des phénomènes électro-magnétiques. On en vint donc progressivement à adopter l’idée d’ondes «immatérielles», représentant la propagation dans «rien» d’un champ considéré comme une simple fonction de l’espace et du temps, c’est-à-dire une entité non visualisable en termes de mouvement. Dans le vocabulaire de l’électromagnétisme, onde et champ ont aujourd’hui complètement perdu leur caractère matériel; le mot onde, employé lorsqu’on veut mettre l’accent sur la propagation du champ, est devenu synonyme de «rayonnement», qui s’oppose à «matière». À la fin du XIXe siècle, la physique connaissait deux types d’ondes: les ondes matérielles, comme les rides à la surface de l’eau ou le son, et des ondes «immatérielles» telles que la lumière et le rayonnement électromagnétique en général. Distinction artificielle en ce sens que les deux types d’ondes, il ne faut pas l’oublier, transportent de l’énergie; de ce point de vue, le rayonnement n’est ni plus ni moins matériel, ou immatériel, que la matière elle-même.2. Détermination du conceptUn concept de l’ordre du continuLa notion d’onde (ou de champ) s’est donc développée en référence – voire en opposition – à celle de particule; elle opère dans l’ordre du continu non dénombrable , alors que le concept de particule relève du discret, dénombrable; c’est d’ailleurs ce dernier concept qui permet de penser la matière en termes atomistes. Alors qu’une particule n’occupe à chaque instant qu’un seul point de l’espace, une onde est caractérisée par son amplitude, définie en tous les points de l’espace-temps. La nature mathématique de la fonction amplitude dépend du type de phénomène que représente l’onde; cela peut être un scalaire – c’est le cas de l’amplitude sonore –, un vecteur – c’est le cas du champ de gravitation newtonienne –, ou un être mathématique plus compliqué, tel un tenseur en gravitation einsteinienne ou l’ensemble de deux champs couplés, en électromagnétisme.Contrairement aux particules qui occupent successivement, au cours du temps, les divers points d’une courbe – leur trajectoire –, les ondes, telles les vagues à la surface de la mer, se déplacent en un mouvement de type frontal ; plus précisément, le lieu des points, où la fonction amplitude 切( る, t ) prend simultanément une même valeur 切, appelée surface d’onde, se déplace au cours du temps, en bloc. Ce mouvement est régi par un ensemble d’équations, appelées «équations d’ondes» ou de propagation, faisant intervenir les dérivées, par rapport aux trois coordonnées d’espace et à celle de temps, de l’amplitude 切( る, t ). Là encore, les ondes font contraste avec les particules: alors que les équations d’ondes sont des équations aux dérivées partielles dont l’une des plus courantes s’écrit:
où désigne la «longueur d’une ondulation» – encore appelée la longueur d’onde – et 嗀 «l’intervalle qui sépare les deux systèmes d’ondes», la différence de marche, dirions-nous aujourd’hui.Ce faisant, Fresnel introduit une échelle dans la notion d’onde, échelle qui justement faisait défaut antérieurement. La longueur d’onde est la longueur caractéristique, l’aune à laquelle doivent être référées toutes les longueurs à considérer dans le phénomène de propagation. Après 1809, les expériences portant sur les ondes se ramèneront toutes à des mesures de longueur d’onde.Dès lors, le concept d’onde est établi en tant qu’objet physico-mathématique; une onde est caractérisée par son amplitude, nombre complexe dont le module est lié à l’intensité et dont la phase régit les combinaisons avec d’autres ondes. À partir de ce moment, les ondes acquièrent un statut ontologique, comparable, bien qu’en un certain sens opposé, à celui des particules.Champ et onde: le concept perd sa «matérialité»À l’origine, le concept d’onde est lié à un mouvement, mouvement vibratoire d’une particule source, provoquant un ébranlement du milieu dans lequel elle se trouve. Dans le cas du son, l’identification de ce milieu ne pose guère de problème: il s’agit de l’air, et la propagation du son s’effectue par mise en branle successive des couches d’air entre la source et le récepteur. «Maintenant, écrit Huygens dans le Traité de la lumière , si l’on examine quelle peut être cette matière dans laquelle s’étend le mouvement qui vient des corps lumineux, laquelle j’appelle éthérée, on verra que ce n’est pas la même qui sert à la propagation du son.» Pendant deux siècles, jusqu’à ce qu’en 1905 Albert Einstein en énonce l’inutilité, le concept d’éther devait apparaître comme indissociable d’abord des ondes lumineuses, puis des ondes électromagnétiques, lorsqu’il fut reconnu que la lumière n’en était qu’une forme particulière.Cet abandon de l’éther, milieu matériel progressivement dépouillé de toutes ses caractéristiques... matérielles, fut grandement facilité, voire suscité, par l’émergence progressive du concept de champ . Initialement, ce dernier est apparu comme un substitut à l’«action à distance», notion aux connotations occultes difficilement acceptables: plutôt que de dire qu’une particule – la Terre par exemple – agit à distance sur une autre – la Lune –, on préféra dire que la première particule induit, par sa seule présence, une modification de l’espace qui l’entoure et que c’est l’effet de cette modification, nommée champ , sur la deuxième qui produit la force que semble exercer à distance la première particule sur la deuxième. De plus, pour éviter d’avoir à penser une action, non seulement «à distance», mais qui plus est instantanée, on en vint à imaginer que le champ se propageait de proche en proche... tout comme une onde, dans un milieu qui, dans la plupart des cas, ne pouvait être que l’éther. Il apparut cependant très vite, avant même qu’Einstein en fasse le constat officiel, que l’éther n’était pas vraiment nécessaire à la compréhension des phénomènes électro-magnétiques. On en vint donc progressivement à adopter l’idée d’ondes «immatérielles», représentant la propagation dans «rien» d’un champ considéré comme une simple fonction de l’espace et du temps, c’est-à-dire une entité non visualisable en termes de mouvement. Dans le vocabulaire de l’électromagnétisme, onde et champ ont aujourd’hui complètement perdu leur caractère matériel; le mot onde, employé lorsqu’on veut mettre l’accent sur la propagation du champ, est devenu synonyme de «rayonnement», qui s’oppose à «matière». À la fin du XIXe siècle, la physique connaissait deux types d’ondes: les ondes matérielles, comme les rides à la surface de l’eau ou le son, et des ondes «immatérielles» telles que la lumière et le rayonnement électromagnétique en général. Distinction artificielle en ce sens que les deux types d’ondes, il ne faut pas l’oublier, transportent de l’énergie; de ce point de vue, le rayonnement n’est ni plus ni moins matériel, ou immatériel, que la matière elle-même.2. Détermination du conceptUn concept de l’ordre du continuLa notion d’onde (ou de champ) s’est donc développée en référence – voire en opposition – à celle de particule; elle opère dans l’ordre du continu non dénombrable , alors que le concept de particule relève du discret, dénombrable; c’est d’ailleurs ce dernier concept qui permet de penser la matière en termes atomistes. Alors qu’une particule n’occupe à chaque instant qu’un seul point de l’espace, une onde est caractérisée par son amplitude, définie en tous les points de l’espace-temps. La nature mathématique de la fonction amplitude dépend du type de phénomène que représente l’onde; cela peut être un scalaire – c’est le cas de l’amplitude sonore –, un vecteur – c’est le cas du champ de gravitation newtonienne –, ou un être mathématique plus compliqué, tel un tenseur en gravitation einsteinienne ou l’ensemble de deux champs couplés, en électromagnétisme.Contrairement aux particules qui occupent successivement, au cours du temps, les divers points d’une courbe – leur trajectoire –, les ondes, telles les vagues à la surface de la mer, se déplacent en un mouvement de type frontal ; plus précisément, le lieu des points, où la fonction amplitude 切( る, t ) prend simultanément une même valeur 切, appelée surface d’onde, se déplace au cours du temps, en bloc. Ce mouvement est régi par un ensemble d’équations, appelées «équations d’ondes» ou de propagation, faisant intervenir les dérivées, par rapport aux trois coordonnées d’espace et à celle de temps, de l’amplitude 切( る, t ). Là encore, les ondes font contraste avec les particules: alors que les équations d’ondes sont des équations aux dérivées partielles dont l’une des plus courantes s’écrit: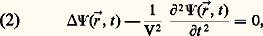 les équations du mouvement des particules sont des équations différentielles ordinaires par rapport à la seule variable t :
les équations du mouvement des particules sont des équations différentielles ordinaires par rapport à la seule variable t :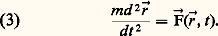 Le principe constitutif de superpositionLa différence entre ondes et particules, leur radicale hétérogénéité, apparaît pleinement lorsqu’on étudie la rencontre de deux ondes. D’ailleurs, c’est en constatant qu’il était impossible de rendre compte du croisement de deux lumières que Huygens a «inventé» le concept d’onde. Imaginons deux ondes d’amplitudes 切1( る, t ) et 切2( る, t ), qui, bien que définies en tout point de l’espace-temps, n’occupent à chaque instant qu’une portion de l’espace de façon sensible; supposons que ces deux ondes s’avancent à la rencontre l’une de l’autre; arrive un moment où leurs deux zones d’amplitude non nulle se superposent. Peut-on alors parler de «deux ondes»? Certainement pas, puisque les ondes sont, par nature, non dénombrables. De ce fait, l’expression «deux ondes» n’a de sens ni avant, ni pendant, ni après la rencontre; on n’a jamais affaire qu’à une seule onde; celle-ci présente deux zones de localisation avant la rencontre, ces deux zones se fondant en une seule pendant tout le temps que dure la «superposition», pour finalement se séparer de nouveau et continuer leur propagation, comme si de rien n’était (fig. 2).C’est ici qu’intervient ce que l’on peut considérer comme le principe constitutif du concept d’onde: le principe de superposition , qui permet de calculer l’amplitude résultant de la combinaison de deux amplitudes 切1( る, t ) et 切2( る, t ). Celle-ci doit évidemment être solution de la même équation d’ondes que 切1( る, t ) et 切2( る, t ). Or, dans la plupart des cas, cette équation est linéaire (voir par exemple celle, citée plus haut, qui régit, entre autres, la propagation du son et des ondes électromagnétiques). Ce n’est d’ailleurs pas là un effet du hasard, car, en physique, on commence toujours par traiter les phénomènes de la façon mathématique la plus simple, ce qui, en l’occurrence, revient à supposer que les lois qui régissent le phénomène sont linéaires – quitte, si l’approximation linéaire s’avère incapable de rendre compte des observations, à passer à l’ordre supérieur d’approximation (voir le cas de l’optique dite non linéaire et des solitons). Les équations d’ondes étant donc, pour cette raison de commodité mathématique, linéaires, leurs solutions le sont également et l’amplitude 切( る, t ) résultante de la combinaison de 切1( る, t ) et 切2( る, t ) s’écrit simplement:
Le principe constitutif de superpositionLa différence entre ondes et particules, leur radicale hétérogénéité, apparaît pleinement lorsqu’on étudie la rencontre de deux ondes. D’ailleurs, c’est en constatant qu’il était impossible de rendre compte du croisement de deux lumières que Huygens a «inventé» le concept d’onde. Imaginons deux ondes d’amplitudes 切1( る, t ) et 切2( る, t ), qui, bien que définies en tout point de l’espace-temps, n’occupent à chaque instant qu’une portion de l’espace de façon sensible; supposons que ces deux ondes s’avancent à la rencontre l’une de l’autre; arrive un moment où leurs deux zones d’amplitude non nulle se superposent. Peut-on alors parler de «deux ondes»? Certainement pas, puisque les ondes sont, par nature, non dénombrables. De ce fait, l’expression «deux ondes» n’a de sens ni avant, ni pendant, ni après la rencontre; on n’a jamais affaire qu’à une seule onde; celle-ci présente deux zones de localisation avant la rencontre, ces deux zones se fondant en une seule pendant tout le temps que dure la «superposition», pour finalement se séparer de nouveau et continuer leur propagation, comme si de rien n’était (fig. 2).C’est ici qu’intervient ce que l’on peut considérer comme le principe constitutif du concept d’onde: le principe de superposition , qui permet de calculer l’amplitude résultant de la combinaison de deux amplitudes 切1( る, t ) et 切2( る, t ). Celle-ci doit évidemment être solution de la même équation d’ondes que 切1( る, t ) et 切2( る, t ). Or, dans la plupart des cas, cette équation est linéaire (voir par exemple celle, citée plus haut, qui régit, entre autres, la propagation du son et des ondes électromagnétiques). Ce n’est d’ailleurs pas là un effet du hasard, car, en physique, on commence toujours par traiter les phénomènes de la façon mathématique la plus simple, ce qui, en l’occurrence, revient à supposer que les lois qui régissent le phénomène sont linéaires – quitte, si l’approximation linéaire s’avère incapable de rendre compte des observations, à passer à l’ordre supérieur d’approximation (voir le cas de l’optique dite non linéaire et des solitons). Les équations d’ondes étant donc, pour cette raison de commodité mathématique, linéaires, leurs solutions le sont également et l’amplitude 切( る, t ) résultante de la combinaison de 切1( る, t ) et 切2( る, t ) s’écrit simplement: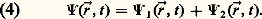 Elle est obtenue par simple addition des composantes . Tel est le contenu du principe dit de superposition. Les deux ondes se superposent simplement, elles gardent leur forme initiale; c’est la raison pour laquelle, une fois passé le temps de la rencontre, les deux ondes reprennent leur cours comme si de rien n’était.La décomposition en ondes harmoniquesLes conséquences du principe de superposition sont immenses; ce principe conditionne entièrement la physique mathématique des phénomènes ondulatoires. En effet, à partir du moment où pour combiner deux ondes il suffit de les additionner, il devient possible, à l’inverse, d’analyser n’importe quelle onde en une somme d’ondes élémentaires que l’on choisira aussi «simples» que possible.C’est ce qu’autorise précisément un théorème mathématique essentiel, le théorème de Fourier , qui s’énonce ainsi: toute fonction 切(t ) d’une variable réelle t peut, moyennant certaines conditions de régularité – que le physicien suppose toujours satisfaites –, être décomposée en une somme de fonctions harmoniques de la variable t , c’est-à-dire en une somme de fonctions du type Cn expi ( 諸n t + 見n ), ou, ce qui revient au même, en une somme de fonctions An cos 諸n t + Bn cos 諸n t :
Elle est obtenue par simple addition des composantes . Tel est le contenu du principe dit de superposition. Les deux ondes se superposent simplement, elles gardent leur forme initiale; c’est la raison pour laquelle, une fois passé le temps de la rencontre, les deux ondes reprennent leur cours comme si de rien n’était.La décomposition en ondes harmoniquesLes conséquences du principe de superposition sont immenses; ce principe conditionne entièrement la physique mathématique des phénomènes ondulatoires. En effet, à partir du moment où pour combiner deux ondes il suffit de les additionner, il devient possible, à l’inverse, d’analyser n’importe quelle onde en une somme d’ondes élémentaires que l’on choisira aussi «simples» que possible.C’est ce qu’autorise précisément un théorème mathématique essentiel, le théorème de Fourier , qui s’énonce ainsi: toute fonction 切(t ) d’une variable réelle t peut, moyennant certaines conditions de régularité – que le physicien suppose toujours satisfaites –, être décomposée en une somme de fonctions harmoniques de la variable t , c’est-à-dire en une somme de fonctions du type Cn expi ( 諸n t + 見n ), ou, ce qui revient au même, en une somme de fonctions An cos 諸n t + Bn cos 諸n t :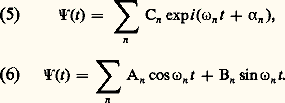 Chaque fonction élémentaire, ou composante de Fourier, est caractérisée par son taux d’évolution en t , qui, lorsque t représente le temps, est appelé «pulsation». L’ensemble des 諸n , intervenant dans la décomposition, forme ce qu’on appelle le «spectre» de 切(t ); celui-ci peut être discret, ou continu. Dans ce dernier cas, la somme discrète écrite ci-dessus doit être remplacée par une intégrale en 諸, ce qui ne change rien sur le fond.Appliquée aux amplitudes ondulatoires, fonctions de る et de t , donc de quatre variables, la décomposition en série de Fourier conduit à exprimer l’amplitude d’une onde quelconque comme une somme d’ondes harmoniques «élémentaires», caractérisées chacune par un ensemble de quatre taux de variation (en t , x , y et z ), et donc par une phase de type:
Chaque fonction élémentaire, ou composante de Fourier, est caractérisée par son taux d’évolution en t , qui, lorsque t représente le temps, est appelé «pulsation». L’ensemble des 諸n , intervenant dans la décomposition, forme ce qu’on appelle le «spectre» de 切(t ); celui-ci peut être discret, ou continu. Dans ce dernier cas, la somme discrète écrite ci-dessus doit être remplacée par une intégrale en 諸, ce qui ne change rien sur le fond.Appliquée aux amplitudes ondulatoires, fonctions de る et de t , donc de quatre variables, la décomposition en série de Fourier conduit à exprimer l’amplitude d’une onde quelconque comme une somme d’ondes harmoniques «élémentaires», caractérisées chacune par un ensemble de quatre taux de variation (en t , x , y et z ), et donc par une phase de type: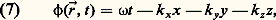 soit encore:
soit encore: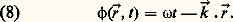 On peut se demander pourquoi les fonctions harmoniques jouent un rôle si important. À cela, deux raisons peuvent être avancées, une d’ordre mathématique, l’autre physique. On démontre en mathématiques que, dans un développement en série de Fourier, la somme des premiers termes est une fonction régulière et que les singularités éventuelles n’apparaissent que si l’on pousse le développement à l’infini; en conséquence, il est possible, pour rendre compte d’une fonction régulière, de se contenter d’un petit nombre de coefficients de Fourier, ce qui est particulièrement agréable. Mais la raison fondamentale du rôle privilégié de la décomposition en série de Fourier tient à la nature régulière, «simple», des fonctions harmoniques. Ces dernières, sans être constantes, ce qui leur ôterait tout intérêt, sont aussi peu changeantes que possible, dans la mesure où un cosinus (ou un sinus) se répète, identique à lui-même, à l’infini. Cette «homogénéité» de variation est évidemment à mettre en rapport avec la linéarité de la phase, et donc avec la constance des taux d’évolution ( 諸 dans le cas du temps, k x , k y , ou k z dans le cas de l’espace). De ce fait, les ondes élémentaires sont périodiques ; par exemple dans le cas du temps:
On peut se demander pourquoi les fonctions harmoniques jouent un rôle si important. À cela, deux raisons peuvent être avancées, une d’ordre mathématique, l’autre physique. On démontre en mathématiques que, dans un développement en série de Fourier, la somme des premiers termes est une fonction régulière et que les singularités éventuelles n’apparaissent que si l’on pousse le développement à l’infini; en conséquence, il est possible, pour rendre compte d’une fonction régulière, de se contenter d’un petit nombre de coefficients de Fourier, ce qui est particulièrement agréable. Mais la raison fondamentale du rôle privilégié de la décomposition en série de Fourier tient à la nature régulière, «simple», des fonctions harmoniques. Ces dernières, sans être constantes, ce qui leur ôterait tout intérêt, sont aussi peu changeantes que possible, dans la mesure où un cosinus (ou un sinus) se répète, identique à lui-même, à l’infini. Cette «homogénéité» de variation est évidemment à mettre en rapport avec la linéarité de la phase, et donc avec la constance des taux d’évolution ( 諸 dans le cas du temps, k x , k y , ou k z dans le cas de l’espace). De ce fait, les ondes élémentaires sont périodiques ; par exemple dans le cas du temps: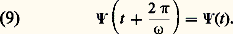 Une période temporelle ou spatiale s’introduit ainsi, liée à 諸, k x , k y , k z , au bout de laquelle l’onde élémentaire reproduit sa forme à l’identique. Autrement dit, le lieu des points où l’amplitude à un même instant prend la même valeur – ce que nous avons appelé front d’ondes – prend, dans ce cas, la forme de plans parallèles et équidistants; d’où l’appellation d’ondes planes données à ces ondes élémentaires . Cette dernière remarque permet de comprendre pourquoi les ondes harmoniques sont privilégiées: elles ont une structure s’accordant avec l’homogénéité supposée de l’espace et du temps; c’est l’un des a-priori essentiels de toute entreprise de théorisation physique. À l’homogénéité du temps répond au niveau des ondes harmoniques un taux d’évolution constant 諸 dans le temps; à l’homogénéité de l’espace dans chacune de ses trois directions correspondent des valeurs bien déterminées des taux d’évolution spatiale, k x , k y et k z .Modulation; vitesses de phase et de groupeOn conçoit, dès lors, que le degré de complexité d’une onde puisse être mesuré par le nombre d’ondes élémentaires que contient sa décomposition en série de Fourier, et donc par le nombre de valeurs du taux d’évolution, en x (pour nous limiter, momentanément à une seule direction, x , de l’espace-temps). Ainsi, la superposition de deux ondes harmoniques, caractérisées par leurs taux d’évolution spatiale k 1 et k 2 – ou encore par leurs «longueurs d’ondulation», ou longueur d’onde1 = 2 神/k l et2 = 2 神/k 2 – donnet-elle une onde qui, si elle se répète bien encore indéfiniment, exhibe néanmoins, à l’intérieur de chaque ondulation, une structure moins simple que celle d’une onde harmonique: l’onde est alors dite modulée (fig. 3). Au fur et à mesure qu’augmente le nombre de composantes de Fourier, passant de 2 à 3, etc., on obtient une onde résultante de moins en moins simple, jusqu’à aboutir, dans le cas d’un spectre continu en k , à une onde qui ne se reproduit même plus d’un bout à l’autre de l’axe des x , mais reste confinée à l’intérieur d’un domaine de largeur x , dont on peut montrer qu’il est d’autant plus restreint que le spectre en k , k , est plus grand ( k . x 力 1).Introduisons maintenant dans l’analyse précédente le temps que nous avions provisoirement éliminé; cela afin d’établir comment se propage une onde complexe, comportant au moins deux composantes de Fourier à la fois en x et en t . Nous observons alors un phénomène curieux: contrairement aux particules pour lesquelles, en tout état de cause, il ne peut être défini qu’une seule vitesse, nous nous voyons contraints d’en définir deux, même dans le cas (fig. 4) d’une onde ne comportant que deux ondes «planes». En effet, observons au cours du temps – en prenant une série de photographies du phénomène à intervalles réguliers – le déplacement d’un point de l’onde; nous constatons qu’au bout du temps qu’a duré l’expérience représentée ce point s’est déplacé d’une distance AB, ce qui définit une première vitesse. Mais n’aurions-nous pas dû considérer plutôt l’évolution dans le temps du phénomène global, c’est-à-dire de la structure qui se répète d’un bout à l’autre de l’axe des x , celle d’un point tel que celui qui est marqué d’une flèche sur la figure? Nous aurions alors obtenu une autre vitesse puisque ce point, durant l’expérience représentée, ne se déplace que de CD. De ce fait, l’onde est bel et bien caractérisée par deux vitesses, l’une – celle du point noir – est dite vitesse de phase et est définie comme le rapport 諸/k ; l’autre – celle du point marqué d’une flèche – est dite vitesse de groupe ; on montre qu’elle vaut, dans le cas présent | 諸2 漣 諸1|/|k 2 漣 k 1|, et de façon plus générale d 諸/dk . Cette dernière vitesse est la vitesse de propagation de l’énergie du phénomène. L’existence de deux vitesses n’a d’ailleurs rien qui surprenne le sens commun et l’observation courante: lorsqu’on examine attentivement les rides à la surface d’une mare dans laquelle on a lancé un pavé, on voit se déplacer, «sous» les rides qui constituent le phénomène principal, des vaguelettes qui vont à une vitesse manifestement différente.Toutes ces descriptions mettent en évidence l’importance de la différence de phase – c’est-à-dire de la valeur que prend la différence ( 諸2t 漣 k 2x ) 漣 ( 諸1t 漣 k 1x ) – dans la superposition des ondes élémentaires. On constate ici, comme l’avait fait Fresnel dans le langage de son temps, que les amplitudes sont des nombres complexes. L’importance de la différence de phase se marque au mieux dans le phénomène dit d’interférence, dans lequel on étudie la superposition, en un même point de l’espace, de deux ondes caractérisées par la même valeur de 諸, mais par des vecteurs や différents. On observe alors une variation d’intensité – définie comme le carré du module de l’amplitude résultante – en fonction du point d’observation [cf. INTERFÉRENCES LUMINEUSES]. Ces variations d’intensité sont régulières et l’on voit apparaître ce qu’on appelle un système de franges. Du point de vue expérimental, c’est là un signe qui ne trompe pas: dès lors qu’on observe des «franges» , on peut être assuré que le phénomène étudié relève de la physique ondulatoire ; il reste à découvrir la nature des amplitudes ondulatoires correspondant au phénomène en question; mais ce qui est sûr, c’est que ce dernier présente un caractère ondulatoire. C’est ainsi que fut, sinon découvert, du moins confirmé le caractère ondulatoire des électrons: on observa des «franges» dans les variations spatiales du nombre d’électrons recueillis après diffusion sur un cristal (expérience effectuée en 1927 par Clinton Davisson et Lester Germer).3. La dualité onde-corpusculePour un physicien de l’âge classique, c’est-à-dire d’avant 1900, les concepts d’onde et de particule apparaissent comme antithétiques; ils sont en quelque sorte complémentaires. Le monde s’interprète par leur jeu combiné; chaque particule émet des ondes auxquelles sont sensibles les autres particules (et vice versa). La distinction entre matière et rayonnement est claire et nette.Cette partition du monde en deux catégories d’objets va être ébranlée par un article d’Einstein paru en 1905. Celui-ci porte un titre surprenant: Sur un point de vue heuristique concernant la production de lumière ... Einstein y démontre que pour l’explication des propriétés thermiques de la lumière, il est nécessaire de considérer l’énergie lumineuse comme générée sous forme de grains, E = h 益 (où h est la constante de Planck et 益 la fréquence de la lumière). En 1909 puis en 1916, Einstein achève de conférer à ces grains un caractère corpusculaire en montrant qu’ils possèdent, comme les particules, une quantité de mouvement. Il montre également que les variations de l’énergie d’un faisceau lumineux font apparaître, côte à côte , un terme qu’on identifie facilement avec les fluctuations d’une onde, et un autre terme qu’on est bien obligé d’interpréter comme une fluctuation du nombre de ces «quanta de lumière», plus tard dénommés photons. Einstein parle alors de dualisme onde-particule.Ce dualisme devait ensuite, dans le courant des années 1920, se transformer en dualité , lorsque Louis de Broglie eut démontré qu’à chaque «atome» de matière doit être associée ce qu’il appela une longueur d’onde (mais qu’il serait plus prudent d’appeler une longueur caractéristique). Celle-ci est liée à la quantité de mouvement (p ) de la particule considérée par la relation, dite de L. de Broglie, p = h /, qui s’écrit encore p = h k /2 神, en posant k = 2 神/ et en identifiant ce k avec un «nombre d’onde». Cette dernière écriture fait apparaître une très forte similitude de forme entre la relation de L. de Broglie et celle de Planck-Einstein, E = h 益. Dans les deux cas, l’écriture est comparable; d’une part, ce sont des concepts corpusculaires (quantité de mouvement ou énergie) et, d’autre part, des concepts «ondulatoires», les guillemets étant là pour rappeler qu’il s’agit en fait d’un abus de langage. Celui-ci se trouva cependant rapidement institutionnalisé, puisque peu après la thèse de Louis de Broglie, l’expérience de Davisson et Germer, déjà citée, apportait une confirmation du caractère «ondulatoire» des électrons. À vrai dire, cet abus de langage initial a longtemps obscurci le débat. L’interprétation de la théorie quantique s’est enlisée durablement dans de fausses questions, du genre: les électrons (ou les photons) sont-ils des ondes ou des particules, des ondes et des particules, quelquefois des ondes et quelquefois des particules, ou bien des ondes se transformant en particules ou des particules se transformant en ondes? La controverse cessa lorsqu’on se résolut à admettre que les concepts classiques d’onde et de particule, munis de leurs déterminations propres, n’avaient plus cours dans ce qu’il est convenu d’appeler le domaine quantique, numériquement délimité par la valeur de la constante de Planck h . Les électrons, les photons et, plus généralement, tous les objets quantiques ne sont ni des ondes ni des particules, mais des objets d’une nature différente, spécifiquement quantique, des quantons .Se pose alors la question de savoir pourquoi certains quantons apparaissent dans les conditions classiques – c’est-à-dire non quantiques – comme de «vraies» ondes, et d’autres comme de «vraies» particules; c’est un fait que les photons forment des ondes (lumineuses) et que les électrons, ou les neutrons, dans le domaine classique sont classés dans la catégorie des particules. C’est ici qu’intervient une seconde dichotomie, purement quantique cette fois-ci, qui partage les quantons en deux catégories: les bosons et les fermions. Cette distinction repose sur la différence de comportement statistique des uns et des autres, lorsqu’ils sont en grand nombre. Alors que certains quantons, les bosons, ont «tendance» à se regrouper, les autres, les fermions, «tiennent à marquer leurs distances vis-à-vis de leurs congénères». Rien d’étonnant, dans ces conditions, à ce que les fermions apparaissent comme des particules dans le domaine classique, alors que les bosons (au nombre desquels figurent les photons, quantons de lumière) se présentent sous l’apparence continue d’une onde. Il faut noter que ce dernier point, s’il correspond bien à l’expérience que l’on a des quantons connus jusqu’à présent, n’est pas encore démontré: il n’existe pas encore de théorème établissant que, dans le domaine classique, les bosons donnent des ondes et les fermions des particules.Désormais, nous utiliserons des notations qui rendent les équations homogènes, et par là même d’écriture plus simple. Autrement dit, alors que dans toute la partie «physique» qui précède, des symboles différents désignaient l’espace ( る) et le temps (t ), liés, comme il se doit, par une vitesse, ici, espace et temps sont rendus homogènes, ce qui revient à dire que la vitesse qui les lie est «prise égale à 1»: x (désignant l’espace) et t ont les mêmes dimensions. De ce fait, les taux d’évolution spatiale et temporelle, distingués jusqu’à présent par deux symboles différents ( 諸 et k ), sont ici tous deux notés k , et nommés «fréquence» (ce qui, si l’on en revient aux conventions des physiciens, revient à «faire 2 神 = 1»).Dans le même ordre d’idées, le sens du mot harmonique est, dans ce qui suit, quelque peu élargi de manière à englober toutes les ondes dont les fréquences sont multiples d’une même fréquence de base, nommée fondamentale.4. Développements récents. Apports des mathématiquesL’étude mathématique des ondes, l’analyse de leur propagation et des interactions qui structurent leur comportement qualitatif ont connu, depuis 1950, un développement spectaculaire. Cela a été permis par la construction de concepts mathématiques et d’outils particulièrement adaptés à l’étude d’équations aux dérivées partielles, telle l’équation des ondes. En retour, l’étude de cette dernière a puissamment contribué à l’élaboration de ces concepts.Principe de superposition et opérateurs intégraux de FourierUn pas important a été effectué par la formalisation du fait que, dans l’équation des ondes:
Une période temporelle ou spatiale s’introduit ainsi, liée à 諸, k x , k y , k z , au bout de laquelle l’onde élémentaire reproduit sa forme à l’identique. Autrement dit, le lieu des points où l’amplitude à un même instant prend la même valeur – ce que nous avons appelé front d’ondes – prend, dans ce cas, la forme de plans parallèles et équidistants; d’où l’appellation d’ondes planes données à ces ondes élémentaires . Cette dernière remarque permet de comprendre pourquoi les ondes harmoniques sont privilégiées: elles ont une structure s’accordant avec l’homogénéité supposée de l’espace et du temps; c’est l’un des a-priori essentiels de toute entreprise de théorisation physique. À l’homogénéité du temps répond au niveau des ondes harmoniques un taux d’évolution constant 諸 dans le temps; à l’homogénéité de l’espace dans chacune de ses trois directions correspondent des valeurs bien déterminées des taux d’évolution spatiale, k x , k y et k z .Modulation; vitesses de phase et de groupeOn conçoit, dès lors, que le degré de complexité d’une onde puisse être mesuré par le nombre d’ondes élémentaires que contient sa décomposition en série de Fourier, et donc par le nombre de valeurs du taux d’évolution, en x (pour nous limiter, momentanément à une seule direction, x , de l’espace-temps). Ainsi, la superposition de deux ondes harmoniques, caractérisées par leurs taux d’évolution spatiale k 1 et k 2 – ou encore par leurs «longueurs d’ondulation», ou longueur d’onde1 = 2 神/k l et2 = 2 神/k 2 – donnet-elle une onde qui, si elle se répète bien encore indéfiniment, exhibe néanmoins, à l’intérieur de chaque ondulation, une structure moins simple que celle d’une onde harmonique: l’onde est alors dite modulée (fig. 3). Au fur et à mesure qu’augmente le nombre de composantes de Fourier, passant de 2 à 3, etc., on obtient une onde résultante de moins en moins simple, jusqu’à aboutir, dans le cas d’un spectre continu en k , à une onde qui ne se reproduit même plus d’un bout à l’autre de l’axe des x , mais reste confinée à l’intérieur d’un domaine de largeur x , dont on peut montrer qu’il est d’autant plus restreint que le spectre en k , k , est plus grand ( k . x 力 1).Introduisons maintenant dans l’analyse précédente le temps que nous avions provisoirement éliminé; cela afin d’établir comment se propage une onde complexe, comportant au moins deux composantes de Fourier à la fois en x et en t . Nous observons alors un phénomène curieux: contrairement aux particules pour lesquelles, en tout état de cause, il ne peut être défini qu’une seule vitesse, nous nous voyons contraints d’en définir deux, même dans le cas (fig. 4) d’une onde ne comportant que deux ondes «planes». En effet, observons au cours du temps – en prenant une série de photographies du phénomène à intervalles réguliers – le déplacement d’un point de l’onde; nous constatons qu’au bout du temps qu’a duré l’expérience représentée ce point s’est déplacé d’une distance AB, ce qui définit une première vitesse. Mais n’aurions-nous pas dû considérer plutôt l’évolution dans le temps du phénomène global, c’est-à-dire de la structure qui se répète d’un bout à l’autre de l’axe des x , celle d’un point tel que celui qui est marqué d’une flèche sur la figure? Nous aurions alors obtenu une autre vitesse puisque ce point, durant l’expérience représentée, ne se déplace que de CD. De ce fait, l’onde est bel et bien caractérisée par deux vitesses, l’une – celle du point noir – est dite vitesse de phase et est définie comme le rapport 諸/k ; l’autre – celle du point marqué d’une flèche – est dite vitesse de groupe ; on montre qu’elle vaut, dans le cas présent | 諸2 漣 諸1|/|k 2 漣 k 1|, et de façon plus générale d 諸/dk . Cette dernière vitesse est la vitesse de propagation de l’énergie du phénomène. L’existence de deux vitesses n’a d’ailleurs rien qui surprenne le sens commun et l’observation courante: lorsqu’on examine attentivement les rides à la surface d’une mare dans laquelle on a lancé un pavé, on voit se déplacer, «sous» les rides qui constituent le phénomène principal, des vaguelettes qui vont à une vitesse manifestement différente.Toutes ces descriptions mettent en évidence l’importance de la différence de phase – c’est-à-dire de la valeur que prend la différence ( 諸2t 漣 k 2x ) 漣 ( 諸1t 漣 k 1x ) – dans la superposition des ondes élémentaires. On constate ici, comme l’avait fait Fresnel dans le langage de son temps, que les amplitudes sont des nombres complexes. L’importance de la différence de phase se marque au mieux dans le phénomène dit d’interférence, dans lequel on étudie la superposition, en un même point de l’espace, de deux ondes caractérisées par la même valeur de 諸, mais par des vecteurs や différents. On observe alors une variation d’intensité – définie comme le carré du module de l’amplitude résultante – en fonction du point d’observation [cf. INTERFÉRENCES LUMINEUSES]. Ces variations d’intensité sont régulières et l’on voit apparaître ce qu’on appelle un système de franges. Du point de vue expérimental, c’est là un signe qui ne trompe pas: dès lors qu’on observe des «franges» , on peut être assuré que le phénomène étudié relève de la physique ondulatoire ; il reste à découvrir la nature des amplitudes ondulatoires correspondant au phénomène en question; mais ce qui est sûr, c’est que ce dernier présente un caractère ondulatoire. C’est ainsi que fut, sinon découvert, du moins confirmé le caractère ondulatoire des électrons: on observa des «franges» dans les variations spatiales du nombre d’électrons recueillis après diffusion sur un cristal (expérience effectuée en 1927 par Clinton Davisson et Lester Germer).3. La dualité onde-corpusculePour un physicien de l’âge classique, c’est-à-dire d’avant 1900, les concepts d’onde et de particule apparaissent comme antithétiques; ils sont en quelque sorte complémentaires. Le monde s’interprète par leur jeu combiné; chaque particule émet des ondes auxquelles sont sensibles les autres particules (et vice versa). La distinction entre matière et rayonnement est claire et nette.Cette partition du monde en deux catégories d’objets va être ébranlée par un article d’Einstein paru en 1905. Celui-ci porte un titre surprenant: Sur un point de vue heuristique concernant la production de lumière ... Einstein y démontre que pour l’explication des propriétés thermiques de la lumière, il est nécessaire de considérer l’énergie lumineuse comme générée sous forme de grains, E = h 益 (où h est la constante de Planck et 益 la fréquence de la lumière). En 1909 puis en 1916, Einstein achève de conférer à ces grains un caractère corpusculaire en montrant qu’ils possèdent, comme les particules, une quantité de mouvement. Il montre également que les variations de l’énergie d’un faisceau lumineux font apparaître, côte à côte , un terme qu’on identifie facilement avec les fluctuations d’une onde, et un autre terme qu’on est bien obligé d’interpréter comme une fluctuation du nombre de ces «quanta de lumière», plus tard dénommés photons. Einstein parle alors de dualisme onde-particule.Ce dualisme devait ensuite, dans le courant des années 1920, se transformer en dualité , lorsque Louis de Broglie eut démontré qu’à chaque «atome» de matière doit être associée ce qu’il appela une longueur d’onde (mais qu’il serait plus prudent d’appeler une longueur caractéristique). Celle-ci est liée à la quantité de mouvement (p ) de la particule considérée par la relation, dite de L. de Broglie, p = h /, qui s’écrit encore p = h k /2 神, en posant k = 2 神/ et en identifiant ce k avec un «nombre d’onde». Cette dernière écriture fait apparaître une très forte similitude de forme entre la relation de L. de Broglie et celle de Planck-Einstein, E = h 益. Dans les deux cas, l’écriture est comparable; d’une part, ce sont des concepts corpusculaires (quantité de mouvement ou énergie) et, d’autre part, des concepts «ondulatoires», les guillemets étant là pour rappeler qu’il s’agit en fait d’un abus de langage. Celui-ci se trouva cependant rapidement institutionnalisé, puisque peu après la thèse de Louis de Broglie, l’expérience de Davisson et Germer, déjà citée, apportait une confirmation du caractère «ondulatoire» des électrons. À vrai dire, cet abus de langage initial a longtemps obscurci le débat. L’interprétation de la théorie quantique s’est enlisée durablement dans de fausses questions, du genre: les électrons (ou les photons) sont-ils des ondes ou des particules, des ondes et des particules, quelquefois des ondes et quelquefois des particules, ou bien des ondes se transformant en particules ou des particules se transformant en ondes? La controverse cessa lorsqu’on se résolut à admettre que les concepts classiques d’onde et de particule, munis de leurs déterminations propres, n’avaient plus cours dans ce qu’il est convenu d’appeler le domaine quantique, numériquement délimité par la valeur de la constante de Planck h . Les électrons, les photons et, plus généralement, tous les objets quantiques ne sont ni des ondes ni des particules, mais des objets d’une nature différente, spécifiquement quantique, des quantons .Se pose alors la question de savoir pourquoi certains quantons apparaissent dans les conditions classiques – c’est-à-dire non quantiques – comme de «vraies» ondes, et d’autres comme de «vraies» particules; c’est un fait que les photons forment des ondes (lumineuses) et que les électrons, ou les neutrons, dans le domaine classique sont classés dans la catégorie des particules. C’est ici qu’intervient une seconde dichotomie, purement quantique cette fois-ci, qui partage les quantons en deux catégories: les bosons et les fermions. Cette distinction repose sur la différence de comportement statistique des uns et des autres, lorsqu’ils sont en grand nombre. Alors que certains quantons, les bosons, ont «tendance» à se regrouper, les autres, les fermions, «tiennent à marquer leurs distances vis-à-vis de leurs congénères». Rien d’étonnant, dans ces conditions, à ce que les fermions apparaissent comme des particules dans le domaine classique, alors que les bosons (au nombre desquels figurent les photons, quantons de lumière) se présentent sous l’apparence continue d’une onde. Il faut noter que ce dernier point, s’il correspond bien à l’expérience que l’on a des quantons connus jusqu’à présent, n’est pas encore démontré: il n’existe pas encore de théorème établissant que, dans le domaine classique, les bosons donnent des ondes et les fermions des particules.Désormais, nous utiliserons des notations qui rendent les équations homogènes, et par là même d’écriture plus simple. Autrement dit, alors que dans toute la partie «physique» qui précède, des symboles différents désignaient l’espace ( る) et le temps (t ), liés, comme il se doit, par une vitesse, ici, espace et temps sont rendus homogènes, ce qui revient à dire que la vitesse qui les lie est «prise égale à 1»: x (désignant l’espace) et t ont les mêmes dimensions. De ce fait, les taux d’évolution spatiale et temporelle, distingués jusqu’à présent par deux symboles différents ( 諸 et k ), sont ici tous deux notés k , et nommés «fréquence» (ce qui, si l’on en revient aux conventions des physiciens, revient à «faire 2 神 = 1»).Dans le même ordre d’idées, le sens du mot harmonique est, dans ce qui suit, quelque peu élargi de manière à englober toutes les ondes dont les fréquences sont multiples d’une même fréquence de base, nommée fondamentale.4. Développements récents. Apports des mathématiquesL’étude mathématique des ondes, l’analyse de leur propagation et des interactions qui structurent leur comportement qualitatif ont connu, depuis 1950, un développement spectaculaire. Cela a été permis par la construction de concepts mathématiques et d’outils particulièrement adaptés à l’étude d’équations aux dérivées partielles, telle l’équation des ondes. En retour, l’étude de cette dernière a puissamment contribué à l’élaboration de ces concepts.Principe de superposition et opérateurs intégraux de FourierUn pas important a été effectué par la formalisation du fait que, dans l’équation des ondes: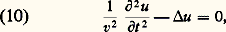 la géométrie du milieu où se propagent les ondes se trouve contenue dans la définition du laplacien de l’onde: u . Si ce milieu est homogène et infini dans toutes les directions spatiales, ce terme s’écrit:
la géométrie du milieu où se propagent les ondes se trouve contenue dans la définition du laplacien de l’onde: u . Si ce milieu est homogène et infini dans toutes les directions spatiales, ce terme s’écrit: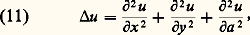 où les coordonnées (x , y , z ) repèrent l’espace. Si ce milieu est localement homogène, mais délimité dans l’espace – appelons-le domaine spatial –, ce terme s’écrit de manière identique, mais l’onde u dont on s’autorise à prendre le laplacien doit vérifier des conditions aux bords de ce domaine: ainsi, lorsque l’onde représente la vibration transversale d’une corde de violon, elle doit s’annuler aux extrémités de la corde; de même qu’elle doit s’annuler aux bords de la membrane d’un tambour lorsqu’elle représente le déplacement transversal de cette membrane. Si l’onde représente la vibration d’une coque de bateau, la géométrie de cette coque se lit dans les coefficients mêmes du laplacien. (Ainsi, le terme v2 dans l’équation, interprété comme constante géométrique, sera dans la suite implicite dans le terme .)En vue d’étudier ces ondes, il est nécessaire d’avoir une formule de représentation des solutions de cette équation. Pour cela, il faut formaliser la notion de rayon lumineux – onde plane –, sachant qu’une localisation simultanée en position et en fréquence est impossible en vertu d’un principe de type Heisenberg. Se laissant guider par le cas où la géométrie est plate – espace usuel – et où la solution est une superposition d’ondes planes de la forme:
où les coordonnées (x , y , z ) repèrent l’espace. Si ce milieu est localement homogène, mais délimité dans l’espace – appelons-le domaine spatial –, ce terme s’écrit de manière identique, mais l’onde u dont on s’autorise à prendre le laplacien doit vérifier des conditions aux bords de ce domaine: ainsi, lorsque l’onde représente la vibration transversale d’une corde de violon, elle doit s’annuler aux extrémités de la corde; de même qu’elle doit s’annuler aux bords de la membrane d’un tambour lorsqu’elle représente le déplacement transversal de cette membrane. Si l’onde représente la vibration d’une coque de bateau, la géométrie de cette coque se lit dans les coefficients mêmes du laplacien. (Ainsi, le terme v2 dans l’équation, interprété comme constante géométrique, sera dans la suite implicite dans le terme .)En vue d’étudier ces ondes, il est nécessaire d’avoir une formule de représentation des solutions de cette équation. Pour cela, il faut formaliser la notion de rayon lumineux – onde plane –, sachant qu’une localisation simultanée en position et en fréquence est impossible en vertu d’un principe de type Heisenberg. Se laissant guider par le cas où la géométrie est plate – espace usuel – et où la solution est une superposition d’ondes planes de la forme: on cherche la solution comme superposition d’ondes élémentaires:
on cherche la solution comme superposition d’ondes élémentaires: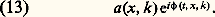 La phase 﨏(t , x , k ) y traduit la géométrie du milieu où l’onde se propage, et la dépendance de l’amplitude a (x , k ) par rapport à la variable de position x découle de la non-homogénéité du milieu. On suppose, comme dans le cas des ondes planes, que la phase est homogène de degré 1 en k , c’est-à-dire (pour réel positif):
La phase 﨏(t , x , k ) y traduit la géométrie du milieu où l’onde se propage, et la dépendance de l’amplitude a (x , k ) par rapport à la variable de position x découle de la non-homogénéité du milieu. On suppose, comme dans le cas des ondes planes, que la phase est homogène de degré 1 en k , c’est-à-dire (pour réel positif):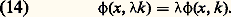 Comme on souhaite faire une analyse en hautes fréquences – c’est-à-dire k «grand» –, on écrit l’amplitude sous la forme d’une somme, infinie, de termes dont l’ordre de grandeur est de plus en plus petit (Peter Lax, 1975):
Comme on souhaite faire une analyse en hautes fréquences – c’est-à-dire k «grand» –, on écrit l’amplitude sous la forme d’une somme, infinie, de termes dont l’ordre de grandeur est de plus en plus petit (Peter Lax, 1975):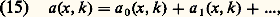
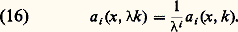 Exiger qu’une telle somme soit solution de l’équation des ondes se traduit alors – après application de l’opérateur des ondes et regroupement des termes homogènes – par l’équation dite eikonale qui fournit la phase:
Exiger qu’une telle somme soit solution de l’équation des ondes se traduit alors – après application de l’opérateur des ondes et regroupement des termes homogènes – par l’équation dite eikonale qui fournit la phase: et par des équations de transport – équations linéaires du premier ordre – qui fournissent les fonctions a i .Ici le signe 瑩. 瑩 exprime la longueur dans la géométrie du milieu considéré. Cette longueur peut dépendre de la position x , ce qui n’est pas le cas dans un milieu homogène où:
et par des équations de transport – équations linéaires du premier ordre – qui fournissent les fonctions a i .Ici le signe 瑩. 瑩 exprime la longueur dans la géométrie du milieu considéré. Cette longueur peut dépendre de la position x , ce qui n’est pas le cas dans un milieu homogène où: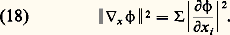 La résolution de l’équation eikonale, équation non linéaire du premier ordre en la variable temporelle t , suppose la donnée de cette phase 﨏 à l’instant t = 0. Afin d’identifier le paramètre k à une fréquence, il est usuel de prendre 﨏(0, x , k ) = x . k , comme dans le cas de l’onde se propageant dans un milieu homogène.On cherche alors la phase en posant
La résolution de l’équation eikonale, équation non linéaire du premier ordre en la variable temporelle t , suppose la donnée de cette phase 﨏 à l’instant t = 0. Afin d’identifier le paramètre k à une fréquence, il est usuel de prendre 﨏(0, x , k ) = x . k , comme dans le cas de l’onde se propageant dans un milieu homogène.On cherche alors la phase en posant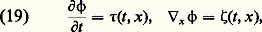 et l’équation eikonale exprime alors que ( 精, 﨣) appartient aux cônes de Monge ( 精2 = 瑩 﨣 瑩2). Le fait que ( 精, 﨣) représente les dérivées premières d’une même fonction, la phase se traduit en disant lagrangienne la surface «étalée au-dessus de l’espace-temps (t , x )» donnée par:
et l’équation eikonale exprime alors que ( 精, 﨣) appartient aux cônes de Monge ( 精2 = 瑩 﨣 瑩2). Le fait que ( 精, 﨣) représente les dérivées premières d’une même fonction, la phase se traduit en disant lagrangienne la surface «étalée au-dessus de l’espace-temps (t , x )» donnée par: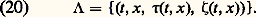 Une branche de la géométrie, dite géométrie symplectique, a pour objet l’étude d’une telle surface.Cette construction faite pour une fréquence k , on écrit la «solution» comme superposition de solutions pour différentes fréquences:
Une branche de la géométrie, dite géométrie symplectique, a pour objet l’étude d’une telle surface.Cette construction faite pour une fréquence k , on écrit la «solution» comme superposition de solutions pour différentes fréquences: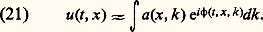 Une telle représentation de l’onde est appelée distribution intégrale de Fourier. Deux faits découlent de cette représentation, comme nous allons le voir.Propagation et optique géométriqueLa construction précédente ayant été faite pour de hautes fréquences – c’est-à-dire k «grand» – ne prend pas en compte ce qui se passe pour de petites valeurs de k . Autrement dit, dans l’écriture de l’onde ci-dessus, ce qui empêche le signe 年 d’être une égalité est une différence pour de petites valeurs de k . Or une telle intégrale, portant sur de petites valeurs de k , est une fonction régulière – c’est-à-dire sans discontinuité, ainsi que ses dérivées. La distribution intégrale de Fourier est donc égale à une onde, à une fonction régulière près. Elle est appelée paramétrixe. Néanmoins, elle a évidemment les mêmes points de discontinuités – singularités – que l’onde u . On montre que les singularités d’une telle intégrale apparaissent aux points où la phase stationne. Si l’on note SS(u ) – SS pour singular set , lieu de singularités – les points où u n’est pas régulière, on a:
Une telle représentation de l’onde est appelée distribution intégrale de Fourier. Deux faits découlent de cette représentation, comme nous allons le voir.Propagation et optique géométriqueLa construction précédente ayant été faite pour de hautes fréquences – c’est-à-dire k «grand» – ne prend pas en compte ce qui se passe pour de petites valeurs de k . Autrement dit, dans l’écriture de l’onde ci-dessus, ce qui empêche le signe 年 d’être une égalité est une différence pour de petites valeurs de k . Or une telle intégrale, portant sur de petites valeurs de k , est une fonction régulière – c’est-à-dire sans discontinuité, ainsi que ses dérivées. La distribution intégrale de Fourier est donc égale à une onde, à une fonction régulière près. Elle est appelée paramétrixe. Néanmoins, elle a évidemment les mêmes points de discontinuités – singularités – que l’onde u . On montre que les singularités d’une telle intégrale apparaissent aux points où la phase stationne. Si l’on note SS(u ) – SS pour singular set , lieu de singularités – les points où u n’est pas régulière, on a: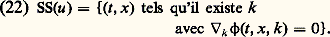 La possibilité d’utiliser ce paramètre k permet même d’affiner la définition des points où l’onde n’est pas régulière. L’onde admet une singularité en (t , x ) dans la direction k 0 si:
La possibilité d’utiliser ce paramètre k permet même d’affiner la définition des points où l’onde n’est pas régulière. L’onde admet une singularité en (t , x ) dans la direction k 0 si: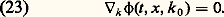 Cet ensemble de points de l’espace-temps et de directions est appelé front d’ondes de u , et noté WF(u ) – WF pour wave front . Cette notion a fait l’objet d’une formalisation algébrique féconde.L’analyse des singularités de la distribution intégrale de Fourier permet de formaliser la notion intuitive de propagation (Lars Hörmander, 1971): si u est singulière en (t 0, x 0, k 0), elle est aussi singulière le long de tout le rayon issu de ce point (t 0, x 0, k 0), et donné par les équations de Hamilton-Jacobi:
Cet ensemble de points de l’espace-temps et de directions est appelé front d’ondes de u , et noté WF(u ) – WF pour wave front . Cette notion a fait l’objet d’une formalisation algébrique féconde.L’analyse des singularités de la distribution intégrale de Fourier permet de formaliser la notion intuitive de propagation (Lars Hörmander, 1971): si u est singulière en (t 0, x 0, k 0), elle est aussi singulière le long de tout le rayon issu de ce point (t 0, x 0, k 0), et donné par les équations de Hamilton-Jacobi: Ainsi apparaissent les rayons de l’optique géométrique, et les surfaces d’ondes classiques. On s’en convaincra en supposant que la géométrie du milieu de propagation est la géométrie usuelle. 瑩. 瑩 est indépendante de la position. On retrouve les rayons rectilignes usuels.Mathématiquement, on subdivise les singularités en deux classes: les singularités C size=1秊, points où l’onde présente une discontinuité en l’une de ses dérivées, et les singularités analytiques, points où l’onde, bien que dérivable à tous ordres, ne peut être développée en série entière. Si, à l’intérieur du milieu, ces singularités se propagent de manière identique – le long des rayons de l’optique géométrique –, nous allons voir qu’il n’en est pas de même lorsqu’un rayon portant une singularité de l’un ou l’autre type atteint le bord du domaine spatial.S’il ne rencontre pas tangentiellement le bord du domaine, il se réfléchit selon les lois de l’optique géométrique et continue à porter le même type de singularité qu’avant la réflexion. Par contre, dans le cas d’un contact tangentiel, une différence essentielle apparaît: si la singularité qu’il porte est une singularité C size=1秊, il continue à se propager de manière rectiligne suivant la tangente au bord. Si la singularité qu’il porte est une singularité analytique, il apparaît une nouvelle singularité analytique qui glisse sur le bord et qui réémet, de chacun de ses points, des rayons sortant tangentiellement du bord et portant aussi des singularités analytiques (fig. 5). L’énergie qu’ils transportent est infiniment petite par rapport au rayon rasant. Cette différence permet de formaliser mathématiquement les notions de diffraction et de pénombre.Qualitativement, on peut observer cette différence en faisant une transformation de Fourier par rapport à la variable temporelle; ce qui mène à l’équation de Helmholtz:
Ainsi apparaissent les rayons de l’optique géométrique, et les surfaces d’ondes classiques. On s’en convaincra en supposant que la géométrie du milieu de propagation est la géométrie usuelle. 瑩. 瑩 est indépendante de la position. On retrouve les rayons rectilignes usuels.Mathématiquement, on subdivise les singularités en deux classes: les singularités C size=1秊, points où l’onde présente une discontinuité en l’une de ses dérivées, et les singularités analytiques, points où l’onde, bien que dérivable à tous ordres, ne peut être développée en série entière. Si, à l’intérieur du milieu, ces singularités se propagent de manière identique – le long des rayons de l’optique géométrique –, nous allons voir qu’il n’en est pas de même lorsqu’un rayon portant une singularité de l’un ou l’autre type atteint le bord du domaine spatial.S’il ne rencontre pas tangentiellement le bord du domaine, il se réfléchit selon les lois de l’optique géométrique et continue à porter le même type de singularité qu’avant la réflexion. Par contre, dans le cas d’un contact tangentiel, une différence essentielle apparaît: si la singularité qu’il porte est une singularité C size=1秊, il continue à se propager de manière rectiligne suivant la tangente au bord. Si la singularité qu’il porte est une singularité analytique, il apparaît une nouvelle singularité analytique qui glisse sur le bord et qui réémet, de chacun de ses points, des rayons sortant tangentiellement du bord et portant aussi des singularités analytiques (fig. 5). L’énergie qu’ils transportent est infiniment petite par rapport au rayon rasant. Cette différence permet de formaliser mathématiquement les notions de diffraction et de pénombre.Qualitativement, on peut observer cette différence en faisant une transformation de Fourier par rapport à la variable temporelle; ce qui mène à l’équation de Helmholtz: Bien entendu, ces phénomènes sont liés à la nature de la condition aux limites du domaine spatial, condition que doit satisfaire l’onde. Si peu de différences apparaissent dans le cas des équations des ondes scalaires, il n’en est pas de même pour des phénomènes décrits par des systèmes.Le cas le plus important dans la pratique est celui du système de l’élasticité. À l’intérieur du milieu, on observe deux types de singularités: l’un correspondant à des ondes vibrant longitudinalement, et se propageant à la vitesse c L, l’autre à des ondes transversales, de vitesse c T. En interagissant avec le bord, les singularités longitudinales et transverses produisent une troisième famille de singularités, résidant sur le bord, et se propageant à la vitesse c R. Ces singularités correspondent aux ondes de Rayleigh et localisent sur le bord la contribution essentielle du phénomène. On a 0 麗 c R 麗 c T 麗 c L. Ce processus est bien connu des spécialistes de la sismique. Dans un tremblement de terre, on perçoit à la surface trois ondes, et c’est la troisième – celle qui arrive le plus tard – qui est la plus dangereuse.Les caustiquesL’analyse des distributions intégrales de Fourier permet de quantifier un second aspect de la propagation lié au phénomène bien connu en optique, les caustiques – du latin causticus , qui brûle. La caustique présente deux propriétés: un déphasage de l’onde qui la traverse et une concentration de l’énergie.Cela découle de la formule de représentation introduite plus haut. La valeur de la phase 﨏, en un point (t , x ) et pour une fréquence k , doit être un point au-dessus de (t , x ) de la surface 炙 «étalée audessus de l’espace-temps». Or cette surface, donnée par la résolution de l’équation eikonale, peut contenir plusieurs valeurs au-dessus du point (t , x ) de l’espace-temps. On est ainsi amené à représenter l’onde par une somme d’intégrales, somme contenant autant de termes qu’il existe de points de la surface lagrangienne au-dessus de (t , x ) [fig. 6]. Si cela ne perturbe pas l’analyse locale faite ci-dessus, il se pose le problème global suivant: que se passe-t-il à la frontière de deux régions de l’espace-temps au-dessus desquelles la surface lagrangienne a un nombre différent de points? Le rang de la projection de 炙 y subit un saut; c’est par ce biais que l’étude de l’équation des ondes rejoint la théorie des catastrophes de René Thom. Cette frontière est une caustique de l’optique géométrique. En vue de raccorder les solutions le long de cette caustique, il est nécessaire d’introduire un déphasage de l’onde, d’un nombre entier de fois 神/4. Ce nombre est l’indice de Maslov, introduit par V. P. Maslov et formalisé par V. Arnold en 1968.Principe de superposition et analyse spectrale: peut-on «entendre» le volume d’un tambour?Un autre aspect de l’étude des ondes a connu, depuis 1912, un développement rapide. Il a été introduit par Hendrik Antoon Lorentz, physicien néerlandais, lors d’une conférence à l’université de Göttingen. Il a été posé dans les termes suivants: dans une région close de l’espace, délimitée par des surfaces parfaitement conductrices, peuvent se former des ondes électromagnétiques stationnaires, analogues aux vibrations de l’air dans un tuyau d’orgue. En ne considérant que les vibrations à hautes fréquences, on constate que le nombre d’harmoniques contenues dans un intervalle de fréquences [v, v + d v] ne dépend pas de la forme de la région, mais uniquement de son volume. Autrement dit, en écoutant les harmoniques à hautes fréquences, peut-on «entendre» le volume d’une région?Il semble que le mathématicien David Hilbert ait pensé qu’il ne verrait pas la preuve de ce résultat de son vivant. Pourtant, Hermann Weyl, qui assistait à la conférence de Göttingen, donnait, dès 1912, la solution de ce problème, grâce à l’étude des opérateurs à noyau intégral qu’il avait effectuée auparavant.Plus précisément, une corde de violon de longueur L – repérée par une variable linéaire x – vibre à des fréquences multiples de 神/L. Pour une telle fréquence – notons la n 神/L –, la vibration est une sinusoïde:
Bien entendu, ces phénomènes sont liés à la nature de la condition aux limites du domaine spatial, condition que doit satisfaire l’onde. Si peu de différences apparaissent dans le cas des équations des ondes scalaires, il n’en est pas de même pour des phénomènes décrits par des systèmes.Le cas le plus important dans la pratique est celui du système de l’élasticité. À l’intérieur du milieu, on observe deux types de singularités: l’un correspondant à des ondes vibrant longitudinalement, et se propageant à la vitesse c L, l’autre à des ondes transversales, de vitesse c T. En interagissant avec le bord, les singularités longitudinales et transverses produisent une troisième famille de singularités, résidant sur le bord, et se propageant à la vitesse c R. Ces singularités correspondent aux ondes de Rayleigh et localisent sur le bord la contribution essentielle du phénomène. On a 0 麗 c R 麗 c T 麗 c L. Ce processus est bien connu des spécialistes de la sismique. Dans un tremblement de terre, on perçoit à la surface trois ondes, et c’est la troisième – celle qui arrive le plus tard – qui est la plus dangereuse.Les caustiquesL’analyse des distributions intégrales de Fourier permet de quantifier un second aspect de la propagation lié au phénomène bien connu en optique, les caustiques – du latin causticus , qui brûle. La caustique présente deux propriétés: un déphasage de l’onde qui la traverse et une concentration de l’énergie.Cela découle de la formule de représentation introduite plus haut. La valeur de la phase 﨏, en un point (t , x ) et pour une fréquence k , doit être un point au-dessus de (t , x ) de la surface 炙 «étalée audessus de l’espace-temps». Or cette surface, donnée par la résolution de l’équation eikonale, peut contenir plusieurs valeurs au-dessus du point (t , x ) de l’espace-temps. On est ainsi amené à représenter l’onde par une somme d’intégrales, somme contenant autant de termes qu’il existe de points de la surface lagrangienne au-dessus de (t , x ) [fig. 6]. Si cela ne perturbe pas l’analyse locale faite ci-dessus, il se pose le problème global suivant: que se passe-t-il à la frontière de deux régions de l’espace-temps au-dessus desquelles la surface lagrangienne a un nombre différent de points? Le rang de la projection de 炙 y subit un saut; c’est par ce biais que l’étude de l’équation des ondes rejoint la théorie des catastrophes de René Thom. Cette frontière est une caustique de l’optique géométrique. En vue de raccorder les solutions le long de cette caustique, il est nécessaire d’introduire un déphasage de l’onde, d’un nombre entier de fois 神/4. Ce nombre est l’indice de Maslov, introduit par V. P. Maslov et formalisé par V. Arnold en 1968.Principe de superposition et analyse spectrale: peut-on «entendre» le volume d’un tambour?Un autre aspect de l’étude des ondes a connu, depuis 1912, un développement rapide. Il a été introduit par Hendrik Antoon Lorentz, physicien néerlandais, lors d’une conférence à l’université de Göttingen. Il a été posé dans les termes suivants: dans une région close de l’espace, délimitée par des surfaces parfaitement conductrices, peuvent se former des ondes électromagnétiques stationnaires, analogues aux vibrations de l’air dans un tuyau d’orgue. En ne considérant que les vibrations à hautes fréquences, on constate que le nombre d’harmoniques contenues dans un intervalle de fréquences [v, v + d v] ne dépend pas de la forme de la région, mais uniquement de son volume. Autrement dit, en écoutant les harmoniques à hautes fréquences, peut-on «entendre» le volume d’une région?Il semble que le mathématicien David Hilbert ait pensé qu’il ne verrait pas la preuve de ce résultat de son vivant. Pourtant, Hermann Weyl, qui assistait à la conférence de Göttingen, donnait, dès 1912, la solution de ce problème, grâce à l’étude des opérateurs à noyau intégral qu’il avait effectuée auparavant.Plus précisément, une corde de violon de longueur L – repérée par une variable linéaire x – vibre à des fréquences multiples de 神/L. Pour une telle fréquence – notons la n 神/L –, la vibration est une sinusoïde: Le nombre de fréquences propres, ou harmoniques, contenues dans un intervalle de fréquences de largeur d v est donc, dans ce cas, de Ld v/ 神; il est bien proportionnel à la longueur de la corde, c’est-à-dire son volume linéaire.Qu’en est-il d’une membrane plane, ou d’un tambour volumique? La clé de cette question réside dans la remarque suivante: dans le cas de la corde de violon, l’onde qui vibre à la fréquence propre n 神/L est une déformation périodique en temps du profil sin(n 神x /L), qui satisfait l’équation:
Le nombre de fréquences propres, ou harmoniques, contenues dans un intervalle de fréquences de largeur d v est donc, dans ce cas, de Ld v/ 神; il est bien proportionnel à la longueur de la corde, c’est-à-dire son volume linéaire.Qu’en est-il d’une membrane plane, ou d’un tambour volumique? La clé de cette question réside dans la remarque suivante: dans le cas de la corde de violon, l’onde qui vibre à la fréquence propre n 神/L est une déformation périodique en temps du profil sin(n 神x /L), qui satisfait l’équation: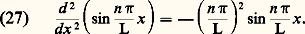 Autrement dit, ce profil ou vibration propre est un vecteur propre de l’opérateur laplacien monodimensionnel 煉2/ 煉x 2, pour une valeur propre égale à l’opposé du carré de la fréquence propre.La question se ramène donc à considérer la fonction: N() = nombre de valeurs propres du laplacien supérieures à 漣.Le résultat de H. Weyl s’énonce alors, en appelant 行 le domaine spatial où se propage l’onde et n la dimension spatiale de 行 – un pour une corde de violon, deux pour une membrane...:
Autrement dit, ce profil ou vibration propre est un vecteur propre de l’opérateur laplacien monodimensionnel 煉2/ 煉x 2, pour une valeur propre égale à l’opposé du carré de la fréquence propre.La question se ramène donc à considérer la fonction: N() = nombre de valeurs propres du laplacien supérieures à 漣.Le résultat de H. Weyl s’énonce alors, en appelant 行 le domaine spatial où se propage l’onde et n la dimension spatiale de 行 – un pour une corde de violon, deux pour une membrane...: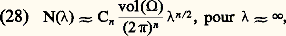 où Cn est le volume de la boule de rayon unité dans l’espace de dimension n . La connaissance du comportement de N(), lorsque tend vers l’infini, fournit donc le volume de 行: on peut «entendre» le volume du tambour.Commentaire sur la méthode d’obtention de ce résultat: curieusement, la méthode mathématique qui permet d’établir ce résultat ne dérive pas de l’étude de l’équation des ondes mais de l’analyse de la diffusion de la chaleur pendant de petites valeurs du temps. Un développement limité complet de l’opérateur de la chaleur est même prouvé, les coefficients traduisant des propriétés géométriques ou topologiques de 行 telles que son volume, la surface de son bord, le nombre de trous qu’il comporte... Mais cet opérateur est lié à N() par la transformation de Laplace, dont l’inverse ne permet de traduire que le premier terme de ce développement sur le comportement, pour grand, de N(). Une raison plus profonde à l’impossibilité de préciser le comportement de N() par les autres termes de son développement limité à l’infini réside dans le fait que le terme qui suit le terme dominant peut présenter des oscillations. Ce comportement ne se déduit pas aisément de la transformée de Laplace. Ces oscillations sont liées à la longueur des rayons périodiques, ou géodésiques périodiques, du milieu où l’onde se propage.Interactions non linéaires d’ondesLe principe constitutif de superposition sans interaction, admis jusqu’ici dans l’exposé des propriétés des ondes, se trouve en défaut lorsqu’on observe la propagation de perturbations à la surface d’un liquide, dans un canal peu profond – équation de Korteweg-de Vries –, ou des signaux électromagnétiques dans un fil infiniment long par rapport à la longueur d’ondes – équation de Boussinesq. Il est donc impossible de rendre compte de tels phénomènes par l’intermédiaire d’une équation linéaire: comme on l’a vu précédemment, linéarité et superposition sans interaction sont synonymes (cf. Le principe constitutif de superposition in chap. 2).Il est alors raisonnable de penser que l’interaction de signaux a dissipé ou créé de l’énergie. Cela conduit à introduire un terme source dans l’équation des ondes, qui dépend de l’onde elle-même et qui ne peut être linéaire:
où Cn est le volume de la boule de rayon unité dans l’espace de dimension n . La connaissance du comportement de N(), lorsque tend vers l’infini, fournit donc le volume de 行: on peut «entendre» le volume du tambour.Commentaire sur la méthode d’obtention de ce résultat: curieusement, la méthode mathématique qui permet d’établir ce résultat ne dérive pas de l’étude de l’équation des ondes mais de l’analyse de la diffusion de la chaleur pendant de petites valeurs du temps. Un développement limité complet de l’opérateur de la chaleur est même prouvé, les coefficients traduisant des propriétés géométriques ou topologiques de 行 telles que son volume, la surface de son bord, le nombre de trous qu’il comporte... Mais cet opérateur est lié à N() par la transformation de Laplace, dont l’inverse ne permet de traduire que le premier terme de ce développement sur le comportement, pour grand, de N(). Une raison plus profonde à l’impossibilité de préciser le comportement de N() par les autres termes de son développement limité à l’infini réside dans le fait que le terme qui suit le terme dominant peut présenter des oscillations. Ce comportement ne se déduit pas aisément de la transformée de Laplace. Ces oscillations sont liées à la longueur des rayons périodiques, ou géodésiques périodiques, du milieu où l’onde se propage.Interactions non linéaires d’ondesLe principe constitutif de superposition sans interaction, admis jusqu’ici dans l’exposé des propriétés des ondes, se trouve en défaut lorsqu’on observe la propagation de perturbations à la surface d’un liquide, dans un canal peu profond – équation de Korteweg-de Vries –, ou des signaux électromagnétiques dans un fil infiniment long par rapport à la longueur d’ondes – équation de Boussinesq. Il est donc impossible de rendre compte de tels phénomènes par l’intermédiaire d’une équation linéaire: comme on l’a vu précédemment, linéarité et superposition sans interaction sont synonymes (cf. Le principe constitutif de superposition in chap. 2).Il est alors raisonnable de penser que l’interaction de signaux a dissipé ou créé de l’énergie. Cela conduit à introduire un terme source dans l’équation des ondes, qui dépend de l’onde elle-même et qui ne peut être linéaire: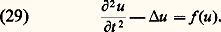 Si l’on s’intéresse à des ondes de faible amplitude, il est légitime de remplacer la non-linéarité f par son équivalent, pour u «petit». Les deux cas suivants peuvent alors se produire:– soit l’interaction dissipe de l’énergie, et le terme source agit alors dans le sens opposé à l’onde:
Si l’on s’intéresse à des ondes de faible amplitude, il est légitime de remplacer la non-linéarité f par son équivalent, pour u «petit». Les deux cas suivants peuvent alors se produire:– soit l’interaction dissipe de l’énergie, et le terme source agit alors dans le sens opposé à l’onde: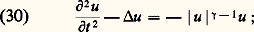 – soit l’interaction crée de l’énergie, et l’équation est alors, pour u positif, du type:
– soit l’interaction crée de l’énergie, et l’équation est alors, pour u positif, du type: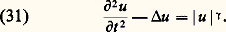 Un problème essentiel réside dans l’analyse de la stabilité de la solution correspondant à l’état de repos, c’est-à-dire de la solution u = 0. Une petite perturbation de cet état à l’instant initial donnera-t-elle lieu à une onde uniformément petite, ou bien mènerat-elle, en certains points du milieu, à une onde d’amplitude arbitrairement grande? Dans le cas où l’onde reste indéfiniment petite, quel est son état ultime, après les états transitoires? Est-il asymptotiquement un état sans interactions? Ce problème est appelé scattering , terme anglais difficile à traduire (dispersion ou diffusion).Les propriétés qualitatives des conditions initiales jouent pour ces problèmes un rôle clé: l’équation des ondes étant différentielle du second ordre en la variable temporelle, sa résolution suppose la connaissance de deux données à un temps pris pour origine temporelle, l’état de l’onde et l’état des vitesses. Ces conditions sont les conditions de Cauchy:
Un problème essentiel réside dans l’analyse de la stabilité de la solution correspondant à l’état de repos, c’est-à-dire de la solution u = 0. Une petite perturbation de cet état à l’instant initial donnera-t-elle lieu à une onde uniformément petite, ou bien mènerat-elle, en certains points du milieu, à une onde d’amplitude arbitrairement grande? Dans le cas où l’onde reste indéfiniment petite, quel est son état ultime, après les états transitoires? Est-il asymptotiquement un état sans interactions? Ce problème est appelé scattering , terme anglais difficile à traduire (dispersion ou diffusion).Les propriétés qualitatives des conditions initiales jouent pour ces problèmes un rôle clé: l’équation des ondes étant différentielle du second ordre en la variable temporelle, sa résolution suppose la connaissance de deux données à un temps pris pour origine temporelle, l’état de l’onde et l’état des vitesses. Ces conditions sont les conditions de Cauchy: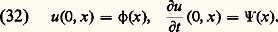 Le problème de la stabilité de la solution nulle, correspondant au milieu au repos, est aisé dans le cas de l’équation des ondes linéaire. Il découle de la conservation de l’énergie:
Le problème de la stabilité de la solution nulle, correspondant au milieu au repos, est aisé dans le cas de l’équation des ondes linéaire. Il découle de la conservation de l’énergie: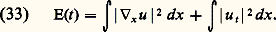 Le premier terme dans cette expression est l’énergie potentielle, le second est l’énergie cinétique. En notant par:
Le premier terme dans cette expression est l’énergie potentielle, le second est l’énergie cinétique. En notant par: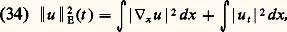 la norme d’énergie de l’onde u , la conservation de l’énergie 林(t ) implique que l’onde u satisfait l’inégalité:
la norme d’énergie de l’onde u , la conservation de l’énergie 林(t ) implique que l’onde u satisfait l’inégalité: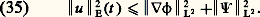 Cette inégalité exprime, que, en mesurant par la norme d’énergie 瑩 . 瑩E la grandeur de l’onde u , cette quantité est contrôlée par la taille de l’énergie à l’origine des temps qui s’exprime en fonction des données de Cauchy.La quantité conservée, dans le cas des équations non linéaires, est:
Cette inégalité exprime, que, en mesurant par la norme d’énergie 瑩 . 瑩E la grandeur de l’onde u , cette quantité est contrôlée par la taille de l’énergie à l’origine des temps qui s’exprime en fonction des données de Cauchy.La quantité conservée, dans le cas des équations non linéaires, est: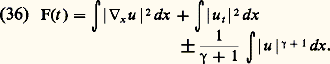 Le signe + correspond à l’équation (30) et le signe 漣 à l’équation (31).La positivité du terme additionnel, dans le cas de l’équation (30), entraîne évidemment que l’énergie de l’onde soit contrôlée, pour tout temps, par la quantité F(0):
Le signe + correspond à l’équation (30) et le signe 漣 à l’équation (31).La positivité du terme additionnel, dans le cas de l’équation (30), entraîne évidemment que l’énergie de l’onde soit contrôlée, pour tout temps, par la quantité F(0): Cela implique que la solution existe pour tout temps, et reste petite.Par contre, l’énergie d’une onde qui satisfait l’équation (31) peut devenir infinie en un temps fini, la conservation de la quantité F traduisant alors que cette énergie explose exactement comme la quantité 咽|u | size=1塚 + 1 dx . Une telle explosion traduit alors un phénomène de focalisation.Enfin, dans le cas de l’équation (30), on peut montrer que, pour de grandes valeurs du temps, l’onde se comporte comme une onde libre – sans interaction – si les données de Cauchy sont suffisamment régulières.Comportement non linéaire et solitonsCertaines équations d’onde non linéaires développent des solutions qui se propagent exactement comme des ondes linéaires: ces ondes, localisées dans l’espace, se déplacent à vitesse constante et sans déformation. De plus, lorsque se rencontrent deux ondes de ce type, elles se séparent après un temps d’interaction et s’éloignent en ayant conservé le même profil que celui qu’elles présentaient avant l’interaction. Elles ont été nommées solitons, la terminaison «on» suggérant un comportement de type particulaire.Un tel phénomène a été observé dès 1834 par Scott Russell, ingénieur de la marine écossaise. Il a remarqué, à l’arrêt brusque d’un bateau dans un canal étroit, la formation à la proue d’une perturbation de l’eau mise en mouvement à une vitesse supérieure à la vitesse caractéristique. L’ayant suivie, sur un cheval au galop, près d’un quart d’heure, il remarqua que son profil restait pratiquement constant: une amplitude de l’ordre d’un mètre à son maximum, la perturbation étant localisée sur une longueur d’une vingtaine de mètres.La formalisation de ce phénomène n’a été accomplie qu’en 1895 par deux scientifiques néerlandais, Korteweg et de Vries. Partant des équations de la mécanique des fluides, et négligeant au deuxième ordre la profondeur du canal devant la longueur d’onde, ils établirent que la surface libre de l’eau devait vérifier:
Cela implique que la solution existe pour tout temps, et reste petite.Par contre, l’énergie d’une onde qui satisfait l’équation (31) peut devenir infinie en un temps fini, la conservation de la quantité F traduisant alors que cette énergie explose exactement comme la quantité 咽|u | size=1塚 + 1 dx . Une telle explosion traduit alors un phénomène de focalisation.Enfin, dans le cas de l’équation (30), on peut montrer que, pour de grandes valeurs du temps, l’onde se comporte comme une onde libre – sans interaction – si les données de Cauchy sont suffisamment régulières.Comportement non linéaire et solitonsCertaines équations d’onde non linéaires développent des solutions qui se propagent exactement comme des ondes linéaires: ces ondes, localisées dans l’espace, se déplacent à vitesse constante et sans déformation. De plus, lorsque se rencontrent deux ondes de ce type, elles se séparent après un temps d’interaction et s’éloignent en ayant conservé le même profil que celui qu’elles présentaient avant l’interaction. Elles ont été nommées solitons, la terminaison «on» suggérant un comportement de type particulaire.Un tel phénomène a été observé dès 1834 par Scott Russell, ingénieur de la marine écossaise. Il a remarqué, à l’arrêt brusque d’un bateau dans un canal étroit, la formation à la proue d’une perturbation de l’eau mise en mouvement à une vitesse supérieure à la vitesse caractéristique. L’ayant suivie, sur un cheval au galop, près d’un quart d’heure, il remarqua que son profil restait pratiquement constant: une amplitude de l’ordre d’un mètre à son maximum, la perturbation étant localisée sur une longueur d’une vingtaine de mètres.La formalisation de ce phénomène n’a été accomplie qu’en 1895 par deux scientifiques néerlandais, Korteweg et de Vries. Partant des équations de la mécanique des fluides, et négligeant au deuxième ordre la profondeur du canal devant la longueur d’onde, ils établirent que la surface libre de l’eau devait vérifier: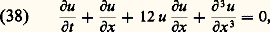 après une normalisation des coefficients qui donne à la vitesse caractéristique la valeur 1.Cette équation admet, pour toute valeur des paramètres a et d , la solution soliton:
après une normalisation des coefficients qui donne à la vitesse caractéristique la valeur 1.Cette équation admet, pour toute valeur des paramètres a et d , la solution soliton: onde spatialement localisée. Pour toute valeur t fixée du temps, son maximum se trouve au point (1 + a 2)t + da , et son amplitude décroît exponentiellement en fonction de la distance à ce maximum.Ce qui différencie foncièrement une telle solution d’une onde linéaire est que sa vitesse dépend de son amplitude, et est supérieure à la vitesse caractéristique. La vitesse (1 + a 2) est la vitesse de l’onde d’amplitude a : l’onde se propage d’autant plus vite qu’elle est plus haute.Mais ces ondes présentent une similarité de comportement avec les ondes linéaires quant à leurs interactions: lorsqu’un soliton rapide rejoint un soliton plus lent, il le dépasse, en conservant sa forme propre, et laisse le soliton lent invariant de forme. L’interaction entraîne simplement à la fois un retard du soliton lent par rapport à sa position dans son mouvement libre et une avance du soliton rapide (fig. 7). Le bon outil qui permet d’établir ce fait est la transformation de Cole-Hopf. Elle consiste à poser:
onde spatialement localisée. Pour toute valeur t fixée du temps, son maximum se trouve au point (1 + a 2)t + da , et son amplitude décroît exponentiellement en fonction de la distance à ce maximum.Ce qui différencie foncièrement une telle solution d’une onde linéaire est que sa vitesse dépend de son amplitude, et est supérieure à la vitesse caractéristique. La vitesse (1 + a 2) est la vitesse de l’onde d’amplitude a : l’onde se propage d’autant plus vite qu’elle est plus haute.Mais ces ondes présentent une similarité de comportement avec les ondes linéaires quant à leurs interactions: lorsqu’un soliton rapide rejoint un soliton plus lent, il le dépasse, en conservant sa forme propre, et laisse le soliton lent invariant de forme. L’interaction entraîne simplement à la fois un retard du soliton lent par rapport à sa position dans son mouvement libre et une avance du soliton rapide (fig. 7). Le bon outil qui permet d’établir ce fait est la transformation de Cole-Hopf. Elle consiste à poser: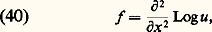 et à chercher f sous forme d’une série entière en un paramètre 﨎:
et à chercher f sous forme d’une série entière en un paramètre 﨎: Écrire que f est solution de (38) et regrouper les termes homogènes en 﨎 conduit alors à une suite d’équations linéaires. La première est:
Écrire que f est solution de (38) et regrouper les termes homogènes en 﨎 conduit alors à une suite d’équations linéaires. La première est: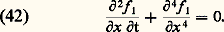 Choisir pour f 1 un unique soliton amène à rendre nuls tous les autres termes du développement. Choisir pour f 1 une somme finie de solitons amène à rendre nuls les termes du développement à partir d’un certain rang. Cette annulation exacte du reste de la série est essentielle et permet de contrôler les termes d’interaction. Ainsi la solution à deux solitons s’écrit:
Choisir pour f 1 un unique soliton amène à rendre nuls tous les autres termes du développement. Choisir pour f 1 une somme finie de solitons amène à rendre nuls les termes du développement à partir d’un certain rang. Cette annulation exacte du reste de la série est essentielle et permet de contrôler les termes d’interaction. Ainsi la solution à deux solitons s’écrit: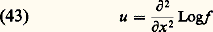 et:
et: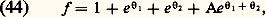 avec:
avec: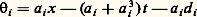 et:
et: Une solution soliton fournit un intéressant contre-exemple à la propriété que possède l’équation des ondes non linéaire (30) énoncée ci-dessus: même arbitrairement petite à l’origine des temps – a «petit» –, une telle solution ne se comporte pas asymptotiquement en temps – t «grand» – comme une solution de l’équation libre, équation linéaire de propagation à la vitesse 1. Sa vitesse de propagation reste inchangée avec le temps et vaut (1 + a 2).L’étude de l’équation de Korteweg-de Vries a été enrichie par son lien au problème de Fermi-Pasta-Ulam. Il s’agit de l’étude numérique réalisée à Los Alamos en 1955, du mouvement de N masses assujetties à rester alignées sur une droite fixe, chacune étant reliée à ses deux voisines les plus proches par des ressorts. Les deux masses extrêmes sont fixes. (Il est intéressant de savoir que ces ondes ont fourni un modèle pour la propagation des erreurs dans les systèmes d’informations complexes.)Si l’on écrit l’équation fondamentale de la dynamique pour ces masses – en notant q n la position de la n e masse sur la droite –, on obtient le système:
Une solution soliton fournit un intéressant contre-exemple à la propriété que possède l’équation des ondes non linéaire (30) énoncée ci-dessus: même arbitrairement petite à l’origine des temps – a «petit» –, une telle solution ne se comporte pas asymptotiquement en temps – t «grand» – comme une solution de l’équation libre, équation linéaire de propagation à la vitesse 1. Sa vitesse de propagation reste inchangée avec le temps et vaut (1 + a 2).L’étude de l’équation de Korteweg-de Vries a été enrichie par son lien au problème de Fermi-Pasta-Ulam. Il s’agit de l’étude numérique réalisée à Los Alamos en 1955, du mouvement de N masses assujetties à rester alignées sur une droite fixe, chacune étant reliée à ses deux voisines les plus proches par des ressorts. Les deux masses extrêmes sont fixes. (Il est intéressant de savoir que ces ondes ont fourni un modèle pour la propagation des erreurs dans les systèmes d’informations complexes.)Si l’on écrit l’équation fondamentale de la dynamique pour ces masses – en notant q n la position de la n e masse sur la droite –, on obtient le système: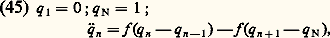 où f modèle la réaction non linéaire d’un ressort. Les réactions considérées sont de la forme: f (x ) = 見x + 廓x 2 ou bien f (x ) = 見x + 廓x 3.L’intuition physique mène à prédire un comportement de ce système tel que l’énergie contenue dans une vibration propre de l’une des masses se transmet aux autres et se répartit, après un régime transitoire, également entre toutes les masses et entre toutes les fréquences propres des ressorts.L’étude numérique a, en fait, montré que cette énergie restait confinée au voisinage de la fréquence propre initiale et que la répartition de cette énergie entre les différentes masses présentait un aspect presque périodique.En pensant n comme une variable continue et en effectuant les changements d’échelle et les approximations adéquates, la dynamique de ce système se trouve régie par l’équation de Korteweg-de Vries.Ondes de chocL’exemple le plus simple d’une onde de choc consiste à formaliser le mouvement de particules le long d’une droite, sans action de forces extérieures. Chaque particule a, à l’origine des temps, une position et une vitesse déterminées. L’équation fondamentale de la dynamique impose que l’accélération de chacune des particules soit nulle, ce qui se traduit, en notant u (t , x ) la vitesse au temps t de la particule qui se trouve à la position x , par l’équation de Burgers:
où f modèle la réaction non linéaire d’un ressort. Les réactions considérées sont de la forme: f (x ) = 見x + 廓x 2 ou bien f (x ) = 見x + 廓x 3.L’intuition physique mène à prédire un comportement de ce système tel que l’énergie contenue dans une vibration propre de l’une des masses se transmet aux autres et se répartit, après un régime transitoire, également entre toutes les masses et entre toutes les fréquences propres des ressorts.L’étude numérique a, en fait, montré que cette énergie restait confinée au voisinage de la fréquence propre initiale et que la répartition de cette énergie entre les différentes masses présentait un aspect presque périodique.En pensant n comme une variable continue et en effectuant les changements d’échelle et les approximations adéquates, la dynamique de ce système se trouve régie par l’équation de Korteweg-de Vries.Ondes de chocL’exemple le plus simple d’une onde de choc consiste à formaliser le mouvement de particules le long d’une droite, sans action de forces extérieures. Chaque particule a, à l’origine des temps, une position et une vitesse déterminées. L’équation fondamentale de la dynamique impose que l’accélération de chacune des particules soit nulle, ce qui se traduit, en notant u (t , x ) la vitesse au temps t de la particule qui se trouve à la position x , par l’équation de Burgers: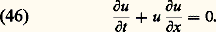 L’état des vitesses, à l’instant t = 0, est donné par u (0, x ) = f (x ). Il est intuitivement clair que ce système générera des chocs lorsqu’une particule rapide rattrapera une particule lente. Mathématiquement, on remarquera que la solution doit être constante, le long de toute droite, dans le plan (t , x ), qui, passant par le point x à t = 0, a pour pente f (x ). Ce sont les caractéristiques non linéaires. Or comme de telles droites peuvent se couper, on est amené à donner à u plusieurs valeurs en un point d’intersection (fig. 8). On observe également que la solution cesse d’être univaluée au moment où une dérivée de la solution est devenue infinie. Cela caractérise les ondes de choc.Ces phénomènes sont repris en détail dans l’ensemble des articles ÉQUATIONS AUX DÉRIVÉES PARTIELLES. Il est cependant important de donner deux faits «structurels». Ce sont les non-linéarités de l’équation d’Euler compressible qui conduisent aux propriétés «physiques» suivantes des solutions:– toute donnée initiale possédant des propriétés de «compression» génère, au bout d’un temps fini, des ondes de chocs;– il existe, en particulier à une dimension d’espace, des solutions qui se décomposent en ondes élémentaires de choc ou de détente;– dans tous les cas, la vitesse et la direction de propagation des phénomènes dépendent non seulement de la structure du problème, mais également des données initiales; cela est dû à la non-linéarité.5. Acquis et états actuelsDans les problèmes d’onde, les variables d’espace jouent un rôle fondamental, bien entendu associé à la notion de propagation. Mais, pour décrire les propriétés des solutions, on est naturellement amené à employer la transformée de Fourier, ce que les physiciens appellent aussi le spectre des solutions.Dans les problèmes linéaires, on rencontre déjà une difficulté fondamentale liée au théorème de Payley Wiener et au principe d’incertitude de Heisenberg. Pour surmonter cette difficulté, les physiciens avaient, au début du siècle, introduit les notions de vitesse de groupe et de vitesse de phase. La contribution des mathématiciens a été la mise au point d’un cadre fonctionnel (front d’ondes, opérateurs Fourier intégraux, etc.) dans lequel la relation entre les phénomènes ondulatoires et corpusculaires s’exprime en négligeant les éléments «réguliers» des solutions. On obtient ainsi à la fois une description plus précise, qualitative, et un outil permettant d’obtenir de nouveaux résultats. Par exemple, la distribution asymptotique des fréquences propres d’un tambour a été décrite plus haut (cf. Principe de superposition ).Dans le cas non linéaire, la situation est beaucoup plus complexe. La transformation de Fourier n’est pas d’usage aussi simple, mais l’aspect analyse de Fourier est cependant toujours présent. En particulier, dans la compétition entre les phénomènes non linéaires et les phénomènes linéaires. Par exemple:a ) dans l’équation de Navier-Stokes, la présence de termes de viscosité empêche la formation de chocs qui se produisent dans l’équation d’Euler;b ) dans l’équation de Korteweg-de Vries, le terme u xxx introduit une dispersion qui empêche également la formation d’ondes de choc;c ) de même, dans les équations d’ondes non linéaires (cf. supra , Interactions non linéaires d’ondes ), c’est la dispersion, liée à l’opérateur , qui empêche la formation de singularités et force la solution à se comporter asymptotiquement comme celle d’un problème linéaire.Ces phénomènes sont extrêmement complexes et, s’ils sont bien décrits dans les cas ci-dessus, en général les notions d’interactions non linéaires et leur influence sur les propagations d’ondes sont mal comprises. Il semble que ce soit dans leur résolution que résident les possibilités de progrès sur des «grands problèmes» comme la description de la turbulence, et c’est pourquoi ils sont au centre des préoccupations des mathématiciens.Sur de tels sujets, l’apparition des ordinateurs a modifié beaucoup les conditions de la recherche, et cela de deux manières complémentaires:– D’une part, une analyse fine des solutions est utile pour réaliser des codes numériques fiables et efficaces.– D’autre part, contrairement à ce qui existait pour les problèmes linéaires, déjà depuis le début du siècle, on ne dispose pas (sauf dans quelques cas particuliers célèbres comme l’équation de Korteweg-de Vries) de problèmes possédant des solutions explicites. Ces exemples explicites sont cependant importants pour guider l’intuition du chercheur. L’ordinateur est alors utilisé pour pallier ce manque et fournir des descriptions qualitatives qui correspondent raisonnablement à la réalité et qui permettent de deviner les propriétés des phénomènes de propagation non linéaires.
L’état des vitesses, à l’instant t = 0, est donné par u (0, x ) = f (x ). Il est intuitivement clair que ce système générera des chocs lorsqu’une particule rapide rattrapera une particule lente. Mathématiquement, on remarquera que la solution doit être constante, le long de toute droite, dans le plan (t , x ), qui, passant par le point x à t = 0, a pour pente f (x ). Ce sont les caractéristiques non linéaires. Or comme de telles droites peuvent se couper, on est amené à donner à u plusieurs valeurs en un point d’intersection (fig. 8). On observe également que la solution cesse d’être univaluée au moment où une dérivée de la solution est devenue infinie. Cela caractérise les ondes de choc.Ces phénomènes sont repris en détail dans l’ensemble des articles ÉQUATIONS AUX DÉRIVÉES PARTIELLES. Il est cependant important de donner deux faits «structurels». Ce sont les non-linéarités de l’équation d’Euler compressible qui conduisent aux propriétés «physiques» suivantes des solutions:– toute donnée initiale possédant des propriétés de «compression» génère, au bout d’un temps fini, des ondes de chocs;– il existe, en particulier à une dimension d’espace, des solutions qui se décomposent en ondes élémentaires de choc ou de détente;– dans tous les cas, la vitesse et la direction de propagation des phénomènes dépendent non seulement de la structure du problème, mais également des données initiales; cela est dû à la non-linéarité.5. Acquis et états actuelsDans les problèmes d’onde, les variables d’espace jouent un rôle fondamental, bien entendu associé à la notion de propagation. Mais, pour décrire les propriétés des solutions, on est naturellement amené à employer la transformée de Fourier, ce que les physiciens appellent aussi le spectre des solutions.Dans les problèmes linéaires, on rencontre déjà une difficulté fondamentale liée au théorème de Payley Wiener et au principe d’incertitude de Heisenberg. Pour surmonter cette difficulté, les physiciens avaient, au début du siècle, introduit les notions de vitesse de groupe et de vitesse de phase. La contribution des mathématiciens a été la mise au point d’un cadre fonctionnel (front d’ondes, opérateurs Fourier intégraux, etc.) dans lequel la relation entre les phénomènes ondulatoires et corpusculaires s’exprime en négligeant les éléments «réguliers» des solutions. On obtient ainsi à la fois une description plus précise, qualitative, et un outil permettant d’obtenir de nouveaux résultats. Par exemple, la distribution asymptotique des fréquences propres d’un tambour a été décrite plus haut (cf. Principe de superposition ).Dans le cas non linéaire, la situation est beaucoup plus complexe. La transformation de Fourier n’est pas d’usage aussi simple, mais l’aspect analyse de Fourier est cependant toujours présent. En particulier, dans la compétition entre les phénomènes non linéaires et les phénomènes linéaires. Par exemple:a ) dans l’équation de Navier-Stokes, la présence de termes de viscosité empêche la formation de chocs qui se produisent dans l’équation d’Euler;b ) dans l’équation de Korteweg-de Vries, le terme u xxx introduit une dispersion qui empêche également la formation d’ondes de choc;c ) de même, dans les équations d’ondes non linéaires (cf. supra , Interactions non linéaires d’ondes ), c’est la dispersion, liée à l’opérateur , qui empêche la formation de singularités et force la solution à se comporter asymptotiquement comme celle d’un problème linéaire.Ces phénomènes sont extrêmement complexes et, s’ils sont bien décrits dans les cas ci-dessus, en général les notions d’interactions non linéaires et leur influence sur les propagations d’ondes sont mal comprises. Il semble que ce soit dans leur résolution que résident les possibilités de progrès sur des «grands problèmes» comme la description de la turbulence, et c’est pourquoi ils sont au centre des préoccupations des mathématiciens.Sur de tels sujets, l’apparition des ordinateurs a modifié beaucoup les conditions de la recherche, et cela de deux manières complémentaires:– D’une part, une analyse fine des solutions est utile pour réaliser des codes numériques fiables et efficaces.– D’autre part, contrairement à ce qui existait pour les problèmes linéaires, déjà depuis le début du siècle, on ne dispose pas (sauf dans quelques cas particuliers célèbres comme l’équation de Korteweg-de Vries) de problèmes possédant des solutions explicites. Ces exemples explicites sont cependant importants pour guider l’intuition du chercheur. L’ordinateur est alors utilisé pour pallier ce manque et fournir des descriptions qualitatives qui correspondent raisonnablement à la réalité et qui permettent de deviner les propriétés des phénomènes de propagation non linéaires.
Encyclopédie Universelle. 2012.
